円錐台の表面積は π × ( r1 r2 )× √(( r1 r2 ) × ( r1 r2 ) 高さ × 高さ ) π × ( r1 × r1 r2 × r2 ) で求めることができます。中1 円錐の表面積 10cm 3cm 10cm 3cm おうぎ形 円 見取図 展開図 円錐を展開すると底面は円,側面はおうぎ形である。動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru

角錐 円錐の体積と表面積の求め方 錐体の公式と母線の概念 リョースケ大学
表面積 円錐の側面積の求め方
表面積 円錐の側面積の求め方- 円錐の体積・表面積 表面積は 0 π です 側面積は 0 π です π=とした時 体積は 0 です 表面積は 0角錐・円錐の体積を出す公式に当てはめると、以下のようになります。 扇形の半径は8cmなので、直径は16cmです。 このとき、1つの四角すいの高さは、立方体の高さの半分になります。 15 底面積と側面積の2つを計算することで、角錐・円錐の表面積を出す




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者
S = πr2 πrl = πr2 πr√r2 h2 S = π r 2 π r l = π r 2 π r r 2 h 2 表面積 = 半径 × 半径 × 314 半径 × 母線の長さ × 314 公式の導出方法と計算例については、「 円錐の表面積の求め方 」をご覧くになります。 中心角 x が分かったので側面積 S が分かります: S = π l 2 × x 360 = π l 2 × r l = π r l 底面積は簡単です。 半径 r の円なので、面積は π r 2 になります。 そして、表面積は側面積+底面積なので、 π r l π r 2 になります。 次回は 円錐の母線次の図形の体積と表面積を求めよ。 (1)底面が1辺6cmの正方形、側面はすべて合同で底辺が6cm、高さが5cmの三角形の四角錐。 また四角錐の高さは4cmとする。 (2)底面が半径5cm、母線が13cm、高さが12cmの円錐。 (1)『体積=底面積×高さ× 1 3 1 3 』なので、 6 ×6 ×4 × 1 3=48cm3 6 × 6 × 4 × 1 3 = 48 c m 3
学習事項:6章 空間図形 円錐の表面積 ・本時の目標 円錐の側面積の求め方について説明することができる。(思) ・本時の展開 教師の働きかけ( )・予想される生徒の反応( ) 留意点( )・評価(※) 1 問題の把握 次の図 予想しよう。(3)この円錐の表面積を求めなさい。 (1)、(2)より、64 π+96 =160 答 160πcm2 (問2)底面の半径6cmで、母線の長さが12c mの円錐について次の問いに答えなさい。 円錐の底面積を求めなさ 円錐 円錐(えんすい,英 cone)とは,円を底面として持つ錐(きり)状にとがった立体のことである‥. Wikipedia先生によると円錐とはこのような立体のことらしいです. 今日は円錐についてのブログです. 表面積を求める公式 S = r π (r m) S = r π (r m)
No012 円錐の体積と表面積 円錐の体積 V m 3 円錐の底面の半径 r m 円錐の高さ h m 円錐の母線の長さ l m 円錐の底面の面積 S 1 m 2 扇形の中心角 θ deg 扇形の周の長さと円錐の底面の円周の長さは等しい 扇形の面積 S 2 m 2 円錐の表面積 S m 2 2 続いて表面積です。 円錐の表面積の公式は「底面積 側面積」でしたね。 底面積は6 × 6 × π = 36π とすぐに出せますね。 続いて、円錐の側面積の求め方は「半径 × π(半径 母線)」でしたね。 よって、側面積の式は 6π(6 10)= 96π となります。 円錐の体積や表面積を求める際にも、円柱の体積や表面積の求め方が大きく関わります。ここでは円柱の体積の求め方を見ていきましょう。 「円柱」の体積を求めてみよう! 例題 底面の円の半径が 3cm 、高さが 8 cm である円柱の体積を求めなさい。




3分でわかる 円錐の体積 表面積の求め方 合格サプリ




中1数学 円すいの問題 練習編 映像授業のtry It トライイット
7 立体の体積と表面積 143 右の図の円錐について,次の問いに答えよ。 ⑴ 底面積を求めよ。 ⑵ 側面の扇形の中心角を求めよ。 ⑶ 側面積を求めよ。 ⑷ 表面積を求めよ。 学基本学習の基本 34 円錐の体積と表面積 問題1 右の図の円錐の体積を求めよ。直円錐(ちょくえんすい) 直円錐とは、底面の円の中心と頂点とを結ぶ線が、底面に垂直である円錐のことです。 図のような母線10cm、半径6cmの直円錐があるとします。 この直円錐の表面積はいくらでしょう? 直円錐を分解 直円錐の底面を外してみました。A = 面積 P = 円周(近似式) 円錐 V = 体積 A = 円錐面積 r = d/2 = 半径 三角錐 V = 体積 S = 角錐底面積 角錐 角錐 pyramid V = 体積 S = 角錐底面積 角錐台 V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径




数学でどうしてもわからない問題があります この円錐の表面積を求め 中学校 教えて Goo




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット
円錐の表面積は、母線×底面の半径×π+底面積なので、12×(10÷2)πで求められます。 なので側面積は、60π㎠です。 底面積は10÷2πなので5π㎠です。 したがって、表面積は(60+5)πで65π㎠です。円錐とそれに内接する球の表面積比と体積比について 球が内接する立体とその内接球について,体積比と表面積比が等しい。 404 円錐とそれに内接する球の表面積比と体積比について – GeoGebra Materials 一覧へ戻る角錐・円錐の体積と表面積の求め方:錐体の公式と母線の概念 ただし、この計算が結構大変です。 解答&解説 この円錐では、半径はわかっていますが、高さがわかりませんね。
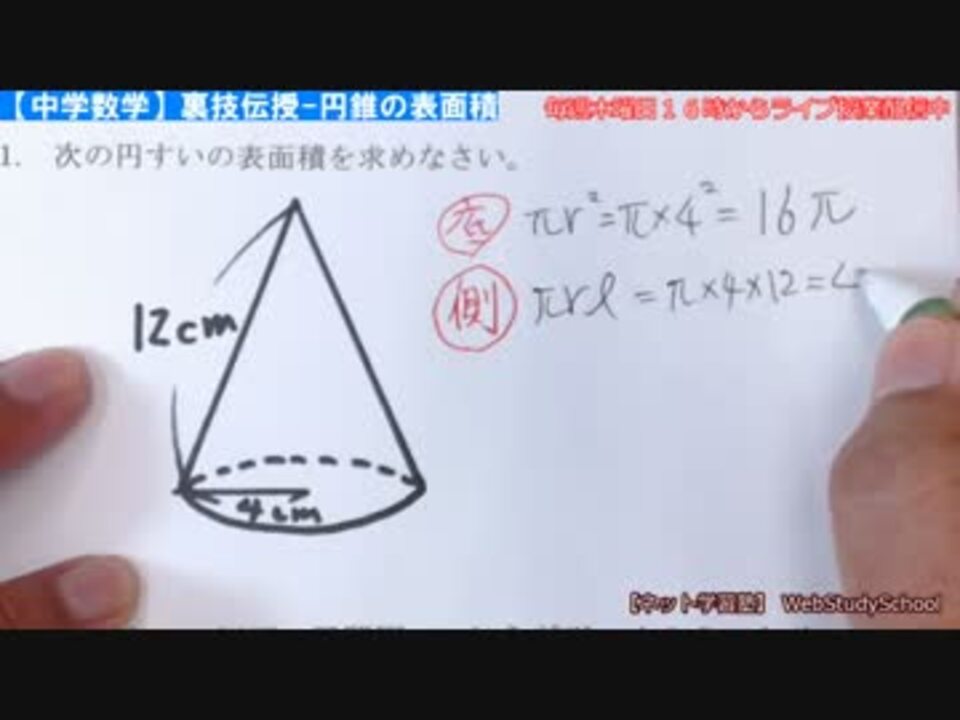



中学数学 裏技伝授 1分で解ける円錐の表面積 中心角の求め方 ニコニコ動画




中学数学の裏技 円錐の表面積を 10秒 で求める方法 Tara Blog
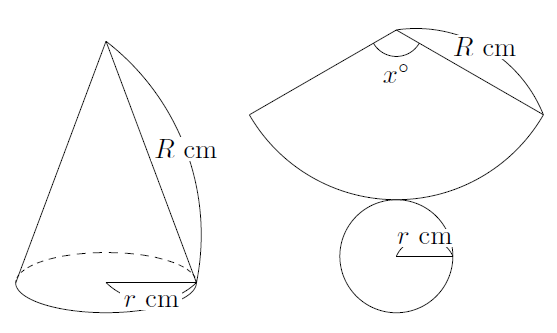
円錐の表面積 底面の半径が r ,母線の長さが R の円錐の表面積を求めるには,右図のように展開図で考え,底面積=円と側面積=扇形の面積を各々求めて加えるとよい. 底面は半径 r の円だから,その面積は πr 2 (1)表面積は、 S = π (a b) (a − b) 2 h 2 π (a 2 b 2)楕円柱の長軸・短軸半径と高さから体積、側面積、表面積を計算します。 直円錐の体積 直円錐の体積 直円錐の半径と高さから体積、側面積、表面積を計算します。 斜切円錐の体積 斜切円錐の体積 直円錐を斜めに切断した体積と切断面積と底面積を計算します。




円錐の表面積 理系ノート




円錐の表面積の求め方を解説 円錐の表面積の求め方は完全パターン化できる
半径2 = 62 −(4√2)2 = 36 −32 = 4 半 径 2 = 6 2 − ( 4 2) 2 = 36 − 32 = 4 ∴ 半径 = 2 半 径 = 2 (半径 > 0 より) これで、 この図になって、これは 最初の問題と同じ だね だから、中心角は1°! はかせちゃん 円錐って英語でcone (コーン)らしいんだけど、 とんがり 円錐の表面積の求め方の公式 って知ってる? 円錐の半径をr、母線の長さをLとすると、円錐の表面積はつぎのように計算できちゃうんだ。 πr(L+r)円柱の表面積を求める問題 円錐の表面積の求め方 問題を学ぶにあたって 今回は、円すい(円錐)が入試に出題されたときに頻出する基本出題パターンをまとめています。以下の10題は、しっかり解き方まで身に着けておきたいものです。



立体 の 表面積 求め 方




円錐の表面積の求め方 裏技の公式を覚えたらめちゃくちゃ簡単 中学や高校の数学の計算問題
側面積=母線×半径×π =9×3×π =27π (㎠) 表面積=9π+27π =36π (㎠) 以上です! めちゃくちゃ簡単じゃないですか? 以上のように、、「円錐の表面積」の問題は 公式1つでとても簡単になります。 それでは今すぐ上の円錐の表面積をよって、表面積は $15π9π=\textcolor{red}{24π\rm cm^2}$ 母線の長さ 問題図のような円錐を、Oを中心に転がすと、 $\textcolor{green}{3}$ 回転してもとの位置に戻りました。 僕は円錐の表面積の求め方は、まず 扇形の弧の長さ=底面の円周なので、 360分のaの「a」を求めます。 aは 扇形の弧の長さが底面の円周と同じ 数字にする為の数字なので、aの計算を 間違えると計算ミスします。




円錐の表面積を簡単に求める方法 Easy Way To Find The Surface Area Of A Cone Youtube




円錐の体積 表面積 側面積 計算機 かんたん計算機
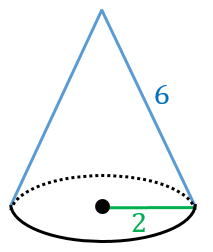



円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学
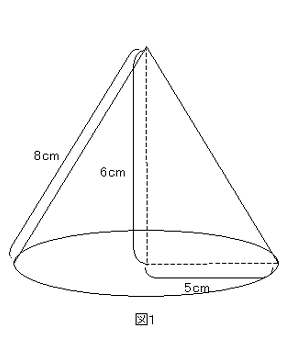



空間図形 練習問題 2 ネット塾




中学数学 円すいの表面積 中学数学の無料オンライン学習サイトchu Su




投影図から円錐の表面積を求める方法がわかりません 答えと解説を詳しく教えてください Clear




中学数学 円錐の高さの求め方 頻出パターン なぜか分かる はかせちゃんの怪しい研究室



Www City Hadano Kanagawa Jp Www Contents Simple Kuukan430 Pdf




円錐の体積ってなんであの公式なの Webty Staff Blog
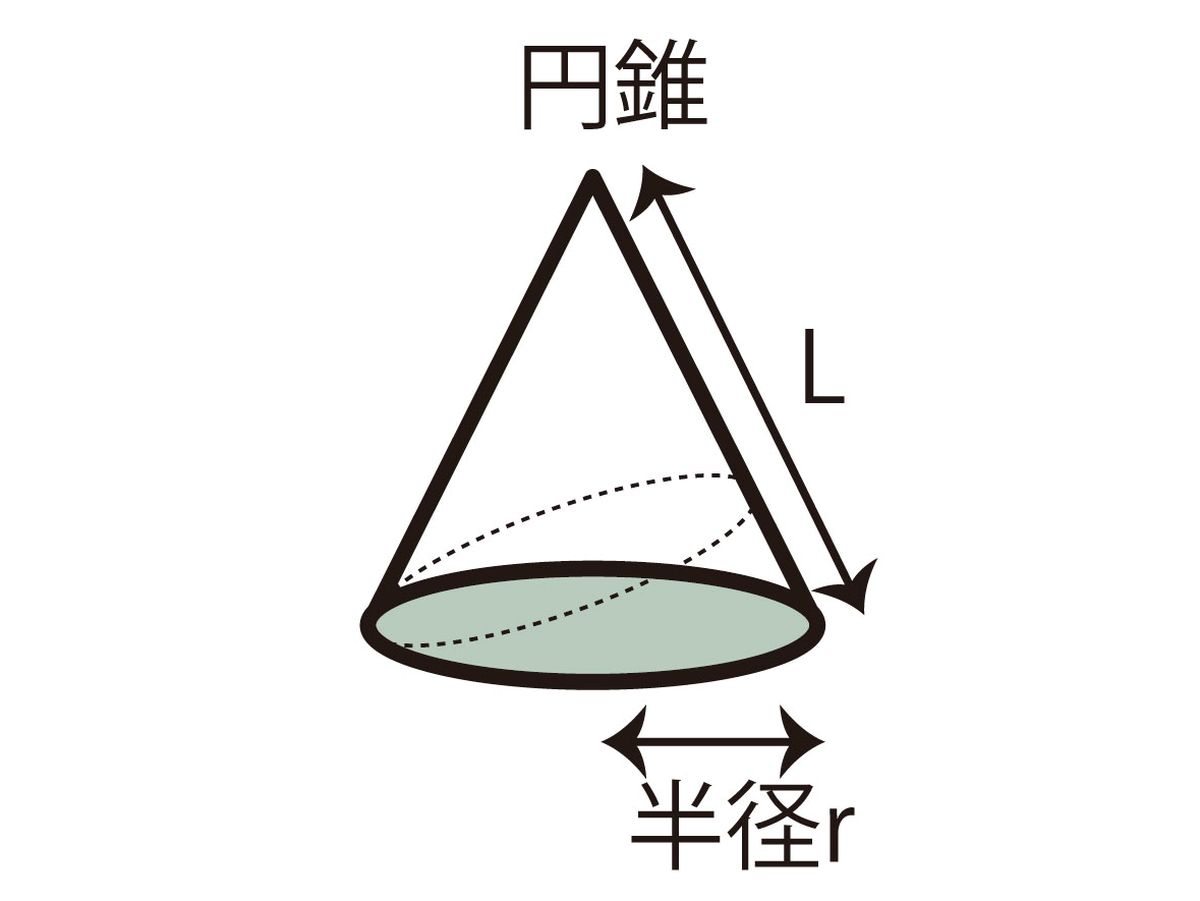



円錐の側面積の公式を理解させる方法 オンライン授業専門塾ファイ




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者




円錐台の側面積の 1 1 3 がよくわかりません なぜ2条にするのですか Clear




角錐 円錐の体積と表面積 計算ドリル 問題集 数学fun




公式を図解 すい体の体積 円すいの表面積の求め方




表面積の求め方 計算公式一覧




円錐の表面積 中心角を求める問題を丁寧に解説 数スタ




円錐の体積と表面積の求め方 押さえておくべき公式と解法の手順




Math 円すいの側面積が1秒で求められる公式 小学生 働きアリ




中学1年生 数学 無料問題集 円すいの表面積 おかわりドリル



球の半分と円錐を組み合わせた立体です 体積と表面積を求めよ 教え Yahoo 知恵袋




計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




球の表面積と体積の公式 数学fun




計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




公式を図解 すい体の体積 円すいの表面積の求め方




現役塾講師直伝 円錐の表面積を求める 裏技 Kouの学び部屋




円錐の表面積の求め方 You Look Too Cool




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット




19年前期 千葉県公立高校入試 数学 第5問 文章題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト
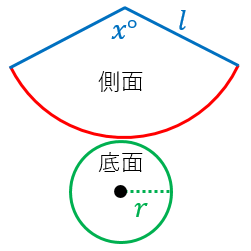



円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学




計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




角錐 円錐の体積と表面積の求め方 錐体の公式と母線の概念 リョースケ大学




円錐の表面積を 公式を使って求める チーム エン




Left 1right 5cm 1ocm Descubre Como Resolverlo En Qanda




中学数学 円錐の裏技集 暗算で中心角 側面積 表面積 中1数学 Youtube




計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




円錐の表面積の求め方 公式と計算例
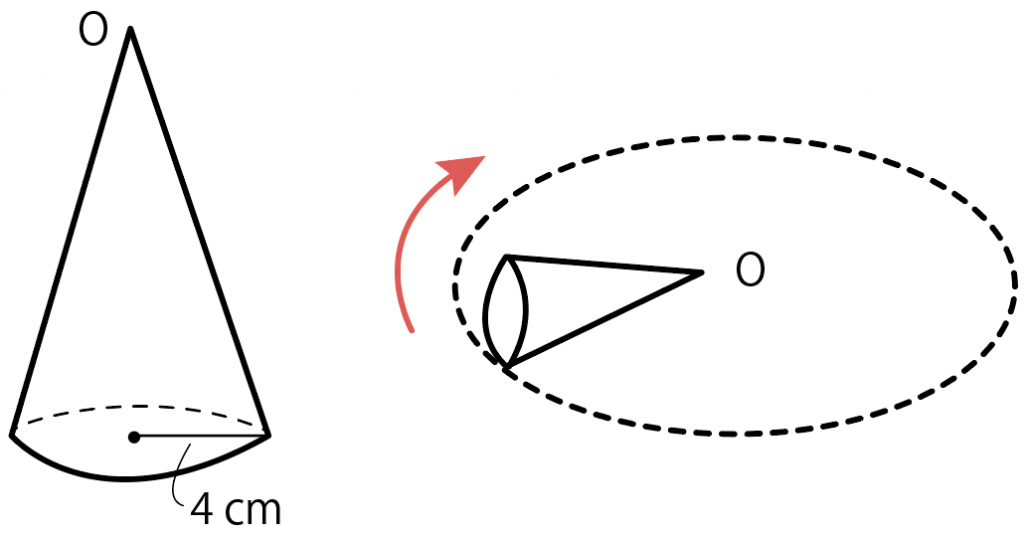



5ステップでわかる 円錐が滑らずに転がる問題の解き方 Qikeru 学びを楽しくわかりやすく




毎日問題を解こう 27 苦手な数学を簡単に




円錐の表面積の求め方 公式と計算例



円錐とは 体積 表面積の公式や求め方 受験辞典
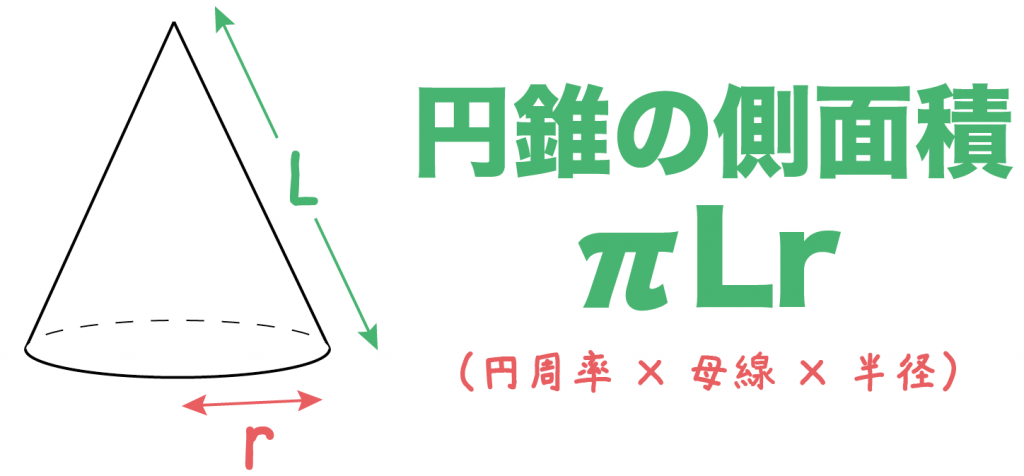



簡単公式 円錐の側面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




円錐の表面積を 中心角を使って求める チーム エン



1




計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



円錐の体積と表面積の求め方を教えてください 錐の体積 1 Yahoo 知恵袋




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット




円錐の表面積 あんず学習塾のメモ 図表置き場




中1数学 円錐の裏技2つ 中学生 数学のノート Clear
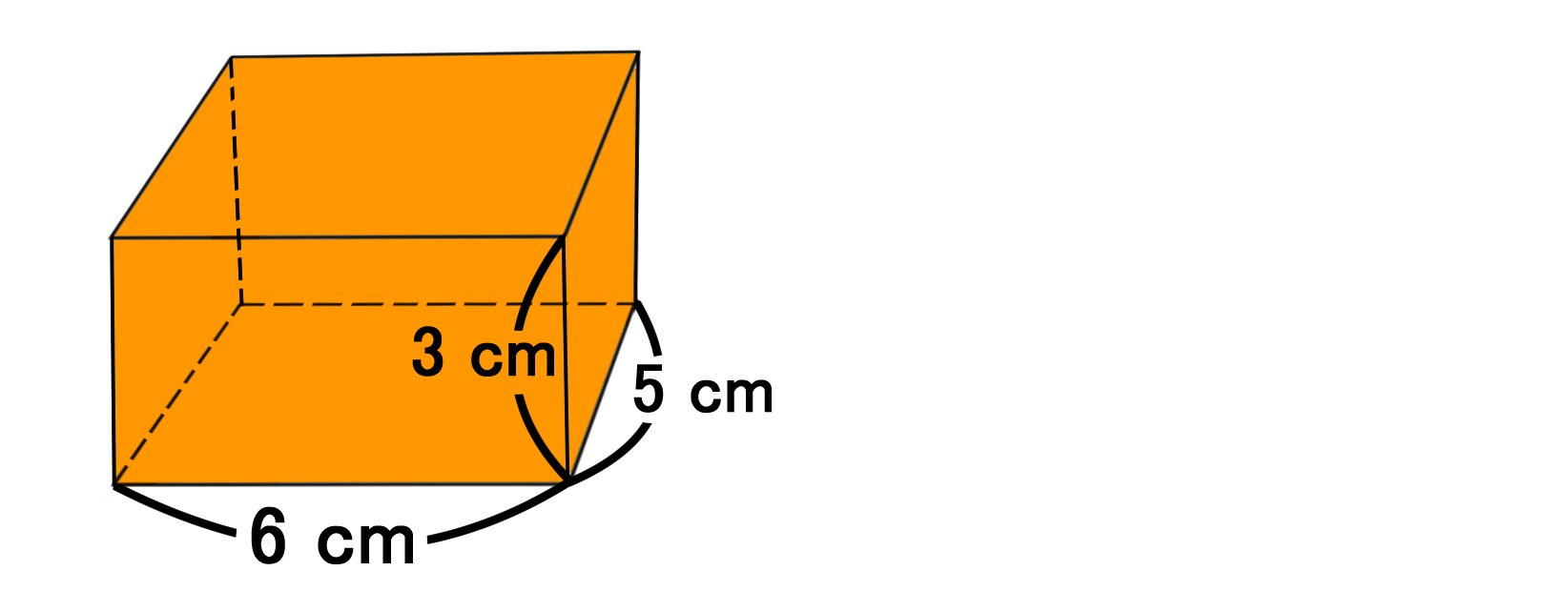



立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学




円錐と円柱の表面積を簡単に求める方法 Easy Way To Find The Surface Area Of Cones And Cylinders Youtube




円柱 円錐 球のcの求め方と公式 高校生向け受験応援メディア 受験のミカタ




この円錐の体積と表面積の求め方を教えてください Clear
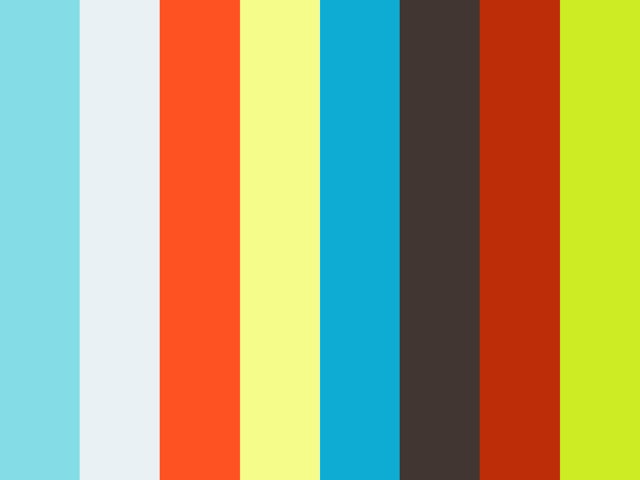



6 17 第6章 空間図形立体の表面積と体積 円錐の表面積 ニュージーランド短期留学ダイアリー



3分でわかる 円錐の体積 表面積の求め方 合格サプリ



Studydoctor円錐の表面積の求め方 中学1年数学 Studydoctor



1



Math 円すいの側面積が1秒で求められる公式 小学生 働きアリ



1




この問題の円錐の底面積の半径の求め方を教えてください Clear




19年前期 千葉県公立高校入試 数学 第5問 文章題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト




円錐の母線 半径 中心角の関係式とそれぞれの求め方 具体例で学ぶ数学




裏ワザ公式 円すいの側面積を一瞬で求める方法 Youtube




円錐の表面積の求め方 公式と計算例




球の表面積と体積の公式 数学fun




立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学




円錐の表面積 Youtube



円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者
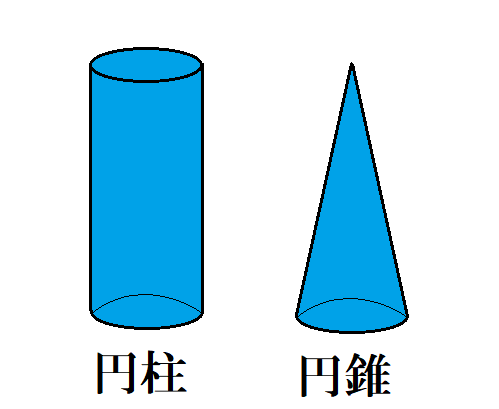



円柱と円錐の違い 表面積や体積 展開図など調べてみたよ ヒデオの情報管理部屋




直円錐を平面で切ったとき 分断される部分の体積と表面積 特殊相対性理論 電磁気学 数学




立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ



中学数学 円すいに関する練習問題



円錐とそれに内接する球の表面積比と体積比について 久保塾 今治市の学習塾



角錐 円錐の表面積 まなびの学園




立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学




公式を図解 すい体の体積 円すいの表面積の求め方
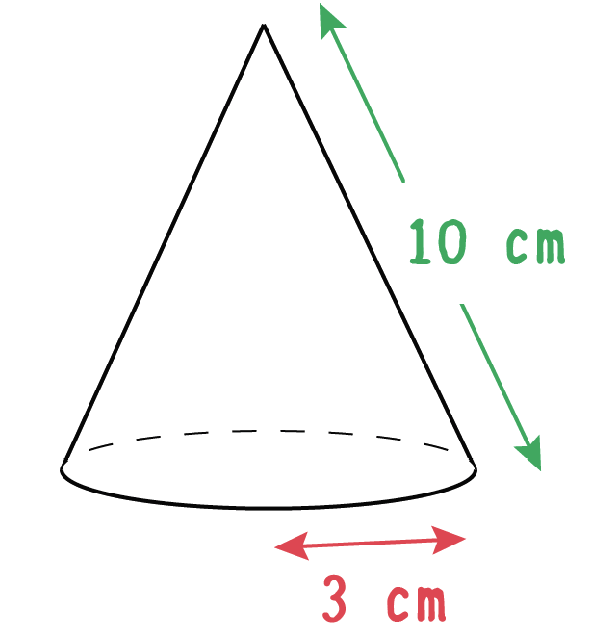



計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



1




円錐の体積の公式 死ぬほど問題に出るので求め方を絶対に覚えよう 中学や高校の数学の計算問題
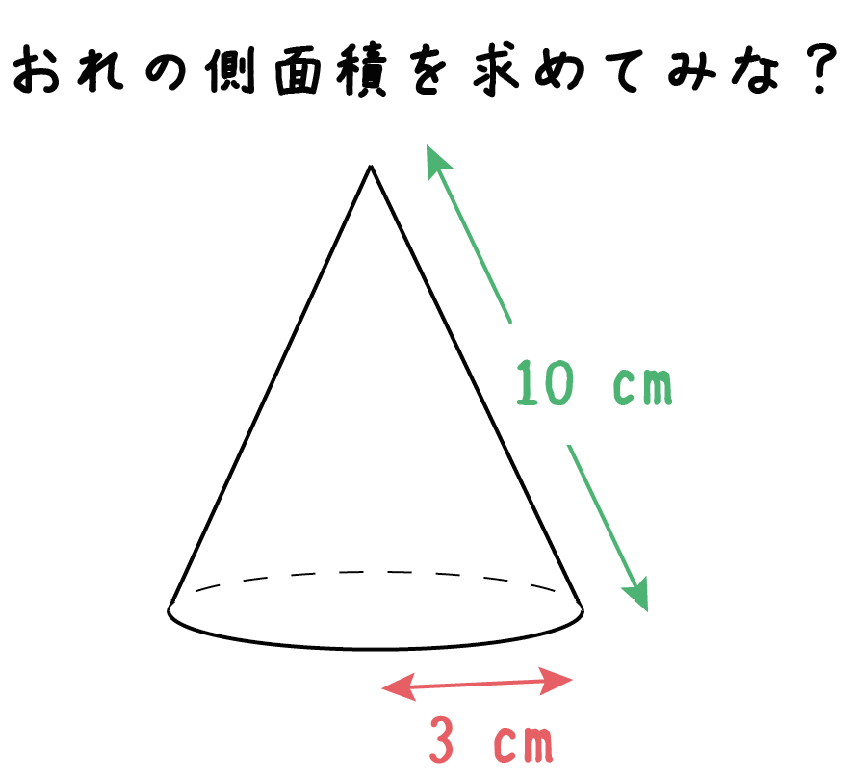



簡単公式 円錐の側面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
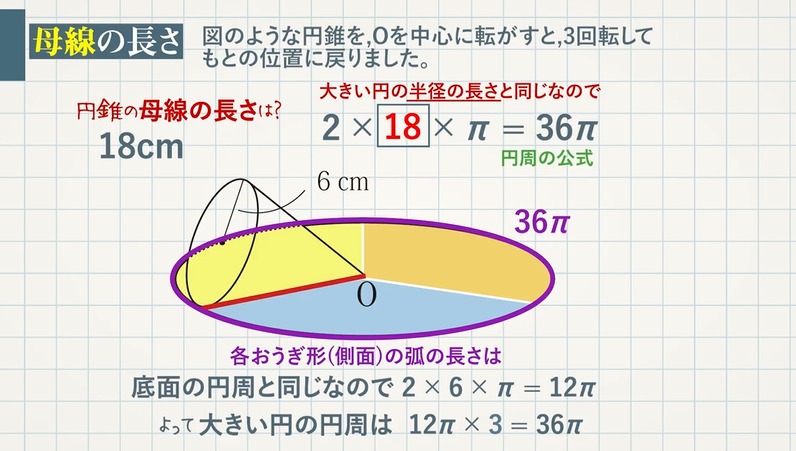



円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者




角錐 円錐の体積と表面積の公式 数学fun




中学数学 円錐の表面積の求め方と公式 図たくさん なぜか分かる はかせちゃんの怪しい研究室




円錐の表面積 簡単な求め方とその理由を解説するぞ 中学数学 理科の学習まとめサイト




円すいの展開図 表面積の求め方 公式があるの知っていますか




円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者
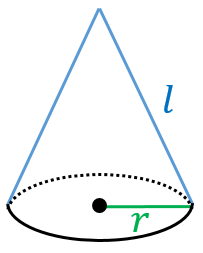



円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学




円錐の表面積 Youtube
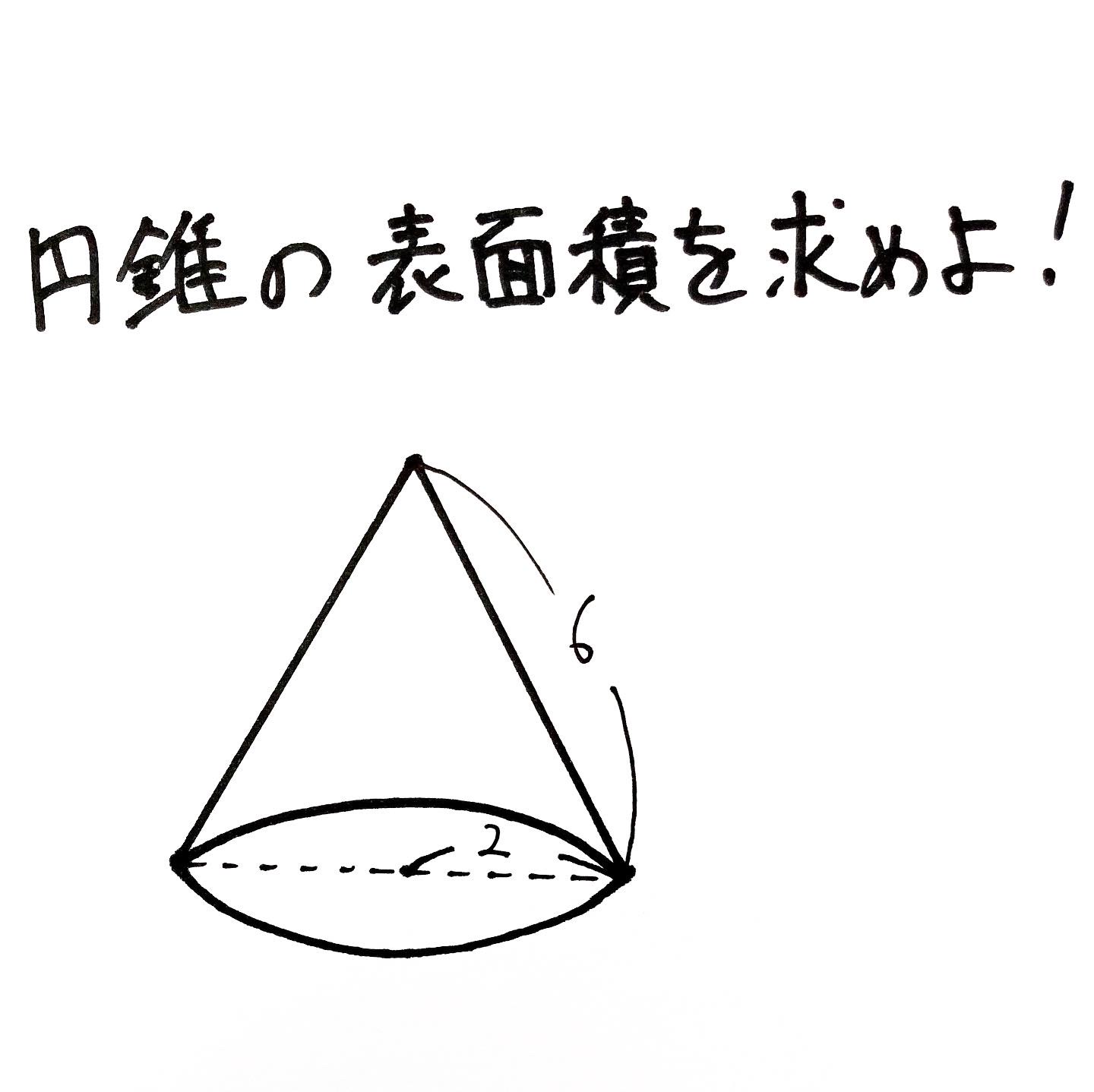



円錐の表面積 完全個別指導の修優舘




公式を図解 すい体の体積 円すいの表面積の求め方



0 件のコメント:
コメントを投稿