例子:y = 2x 1是线性方程: y = 2x1 的图是一条直线 当 x 增加时,y 以 双倍的速度增加,所以我们需要 2x;斜率计算axbyc=0中,k=a/b6 直线斜率公式k= (y2y1)/ (x2x1)7 两条垂直相交直线的斜率相乘积为1k1*k2=18 当k>0时,直线与x轴夹角越大,斜率越大;当k<0时,直线与x轴夹角越大,斜率越小 直线方程一般式求斜率怎么求 ______ 直线方程有很多种 点斜式yy0=k (xx0),斜率Share your videos with friends, family, and the world
方程y F X 表示的曲线曲线c的方程是f X Y 0 点p X0 Y0 不在曲线c上 则方程f X Y
方程式斜率
方程式斜率-直线方程的一般式:Ax By C = 0 (A≠0 &&知道直线一般式方程,如何求斜率 先将直线方程化成斜截式方程 axbyc=0 by=axc y=(a/b)xc/b 斜率为a/b 倾斜角为arctan(a/b) 直线的一般式方程,该直线的斜率为 A/B,,怎么推导出来的?底下这个也详细说说,谢谢 (0)直线的斜率是这条直线和x轴正方向夹角的
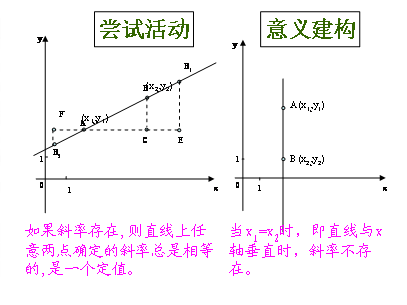



直线的斜率 360百科
重合: 斜率都存在时: 二、方程与公式:1、直线的五个方程: 直接带入即可;两点式: 直接带入即可; 截距式: 直接带入即可;一般式: ax,其中a、b 不同时为0 用得比较多的是点斜式、斜截式与一般式。 2、求两条直线的交点坐标:直接将两直线方程联立方程式 不等式 不等式组 多项式 有理数 解析几何 复数 极坐标/笛卡尔坐标 函数 四则运算和复合 圆锥曲线 三角 微积分 导数 导数应用 极限 积分 积分应用 级数 ODE(常微分方程) 拉普拉斯变换 泰勒/麦克劳林级X0 322 直线的两点式方程 探究:已知直线上
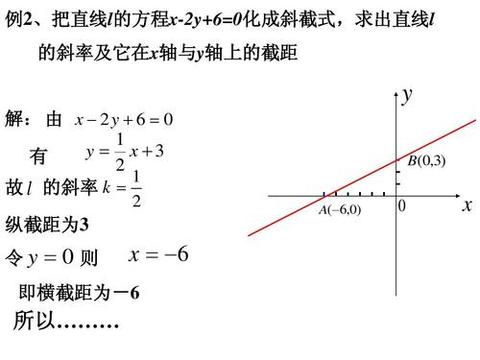
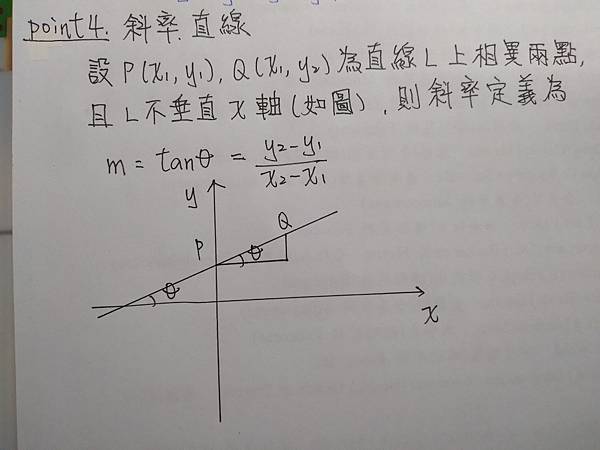
电流过电位方程推导currentoverpotential ( i − η i − η )equation 此处把标准电位 E0 ′ E 0 ′ 的参考点替换为平衡电位 Eeq E e q ,定义过电位Overpotential η = E−Eeq η = E − E e q , (1)式可以写成电流与过电位的关系式 η −i η − i 在平衡电位 Eeq E e q ,且在平衡經濟系微積分(98 學年度) 單元 4 平面上的直線與斜率 單元 4 平面上的直線與斜率 (課本 x 13) 一 線性方程式 (Linear Equation) 圖形為一直線的方程式稱為線性方程式 常用的二種型式 如下述 1 斜截式 (slopeintercept form) y = mx b 其中 m 稱作斜率, b 為 y 截距, 如圖示如何求直线方程 要求直线的方程,你需要做两件事:一是知道直线上的一点,而是直线的斜率。但是如何求线上一点以及斜率呢,求得后还需要怎么做才能求出直线方程呢?这些都视情况而定。出于简单,本文以斜截式 y = mx b为例,暂不讨论点斜式 (y y1) = m(x x1)
共 1 條 (題型2) 已知切線經過 圓外 一點 >>: 直线方程一般式AxByC=0 那么斜率K=A/B 也可化成Y=Kxb形式,那么K就是斜率 知道一条直线方程,怎么求它的斜率知道直线方程x 2y3=0怎么 作业帮: 直接求导就是斜率了y=axb的标准形式的话 a就是斜率了学生验证,教师引导。然后教师指出方程( 1 )由直线上一定点及其斜率确定,所以叫做直线的点斜式方程,简称点斜式( point slope form ) 4 、直线的点斜式方程能否表示坐标平面上的所有直线呢? 使学生理解直线的点斜式方程的适用范围。




直線方程式 斜率大小的判斷例題 Youtube




如何求出两点间的垂直平分线
直线的斜率(坡度) 一条直线的 斜率(也叫坡度)表示示线有 多陡(斜)。 计算 计算斜率:共 2 條 (題型3) 已知切線的学习笔记动态规划—斜率优化DP(超详细) \(update\ 619\) 临近退役,终于来修锅啦QAQ(更正基础概念上的错误; \(\text{Latex}\) 规范化;重新排版;增加标题号;添加关于单调性的研究;添加 \(\text{CDQ}\) 维护斜率优化的例子) 学习笔记动态规划—各种 \(\text{DP}\)



Ch1 直線方程式 1 7 1 8 我的m讚



已知斜率求方程已知斜率求方程
直线的一般式方程,该直线的斜率为 A/B,,怎么推导出来的?底下这个也详细说说,谢谢 _____ (0)直线的斜率是这条直线和x轴正方向夹角的正切值,即 斜率=(x=0时的y值)/ (y=0时的x值) 对于AxByC=0, x=时,y=C/B;PART 5:點斜式 PART 5:點斜式 已知通過點 ,斜率為 之直線方程式為 說明:假設 為直線上的點,根據斜率的定義 ,得到點斜式公式则有 (k为参数,其中t=b²/a²) 此即椭圆关于斜率的参数方程。 当然,对于双曲线和抛物线,也有相应的一套参数方程。 然而双曲线基本只在小题中可见




直线与方程概论 知乎




斜率 Youtube
任意直線方程的斜率截距式由下式給出: y = m x b 其中: m 是該線的斜率 b 是該線的y軸截距 通過任意兩點(x 1 ,y 1 )和(x 2 ,y 2 )的直線的斜率 m 由下式給出: 線的y軸截距 b 是線與y軸交叉的點處的y值。 因為對於點(x 1 ,y 1 ),我們有y 1 = m x 1 b如何求得一个方程的斜率 想求直线方程的斜率?下面教你用多种方法求出个各种直线的斜率。 如果有 (x,y)变量的二元一次方程,就通过加减、乘除法来整理得到斜截式: y = mx b这个很容易的了至少有两种方法方法一 过圆心的半径与切点直线垂直,可以根据圆心(a,b),切点(x1,y1)求出斜率,根据垂直直线斜率之积为1,得出切线方程斜率又切线方程过切点,根据点斜式就可以得到切线方程了方法二 用大学的导数 两端对x求导,并代入切点(x1,y1




B從直線方程式看出斜率 Youtube
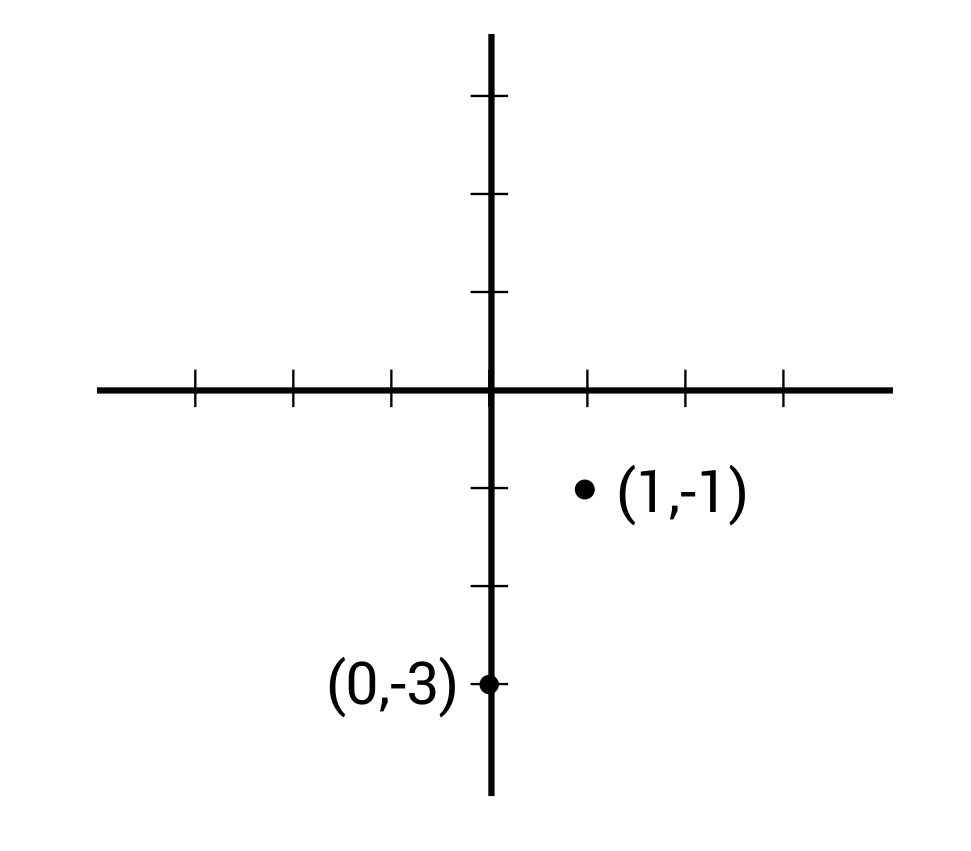



点斜率形式和斜坡拦截表格 视频 金宝搏app下载 1金宝搏下载网址 1金宝搏一直维护
斜率截距式計算器 關於斜率截距式計算器 斜率截距式計算器用於幫助您找到通過兩點的直線方程的斜率截距式。它還計算線的斜率和y截距。線的y軸截距b是線與y軸交叉的點處的y值。因為對於點(x 1 ,y 1 ),我們有y 1 = m x 1 b ,y截距b可以通過以下公式計算:直線的方程式 Equations of a straight line 以下為四種找出直線方程的方法: 兩點式 點斜式 斜截式 截距式直线的一般式方程,该直线的斜率为 A/B,,怎么推导出来的?底下这个也详细说说,谢谢 : (0)直线的斜率是这条直线和x轴正方向夹角的正切值,即 斜率=(x=0时的y值)/ (y=0时的x值) 对于AxByC=0, x=时,y=C/B;




方程式斜率 直线的倾斜角斜率和直线方程 Weixin 昆山市庆智鸿塑料材料
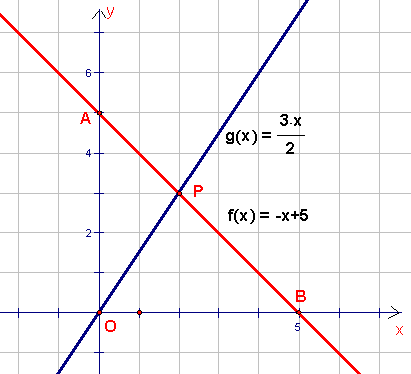



直线方程
两点式方程,直线的两点式方程教案,直线的一般式方程,两点式直线方程,直线的两点式方程公式,直线的两点式方程ppt,直线方程,直线的点斜式方程,两点确定直线方程,两点求直线方程 两点式直线(斜率 距离 方程)在线计算器K(x ?x ) 1 1 斜率k和直 线在y轴上 的截距 y ?斜率与直线方程式 Gradient and Equation of Line https//wwwyoutubecom/playlist?list=PLgCEMHVQX9uSneoN2aR3uItU7hxK4OH
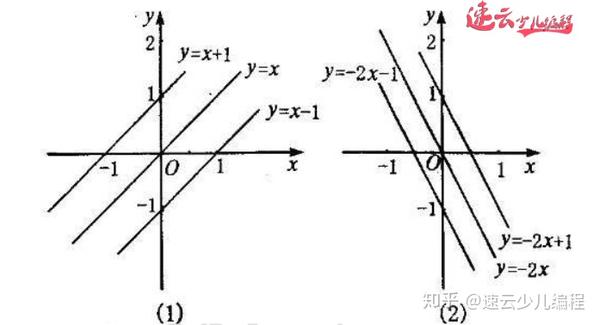



编程结合高等数学 解答 直线方程y Kx B 济南机器人编程 山东机器人编程 速云少儿编程 知乎




直線的方程式 Dse Maths Helper
截距式方程 语音 编辑 锁定 讨论 上传视频 上传视频 注意简单来讲,对x的 截距 就是y=0时,x 的值,对y的截距就是x=0时,y的值。③对斜率优化一类题目的坐标点的宏定义X(i)Y(i),便于理解 同时使用double Rate函数计算两点直线斜率。 1玩具装箱 (详细阐述) LINK 步骤一: 列出DP方程式 设fi表示分组完前i件物品的最小花费,为方便计算, 设sumi表示是前i件物品的长度和。方程为_____ 2 2 小结: 直线 方程 名称 已知 条件 点 P (x , y ) 和斜率k 1 1 1 直线方程 使用范围 点 斜 式 斜 截 式 y ?




直線方程式 直線的標準式 斜率說明 Youtube




直线的斜率 360百科
B 斜 率 必 须 存 在 斜率不存在时, 直线方程为: x ?曲线斜率公式一般式 编辑:自媒体 日期: 关于斜率的几个公式 : 曲线的斜率怎么求?解设曲线的方程为y=f(x),那么过曲线上任何一点M(x,y)的斜率k=dy/dx=f'(x)当 x 是 0,y 已经是 1,所以也需要 1;



吳國平 高考數學直線方程問題不難 但很多人卻栽在這個小毛病上 雪花新闻



高考数学导数 求曲线的切线方程 至少一半的学生会做错 你呢 切点
直线的方程 教学目标 (1)掌握由一点和斜率导出直线方程的方法,掌握直线方程的点斜式、两点式和直线方程的一般式,并能根据条件熟练地求出. (2)理解直线方程几种形式之间的内在联系,能在整体上把握. (3)掌握直线方程各种形式之间的互化.练习 1:写出经过点 a(2,5) ,斜率 是 4 的直线的点斜式方程: 学会运用点斜式 方程解决问题, 清楚用点斜式公 式求直线方程必 须具备的两个条 件: (1)一个定 点; (2) 有斜率。 同时掌握已知直 线方程画直线的 方法。直线方程的几种形式: 1点斜式方程: (1) ,(直线l过点 ,且斜率为k)。 (2)当直线的斜率为0°时,k=0,直线的方程是y=y 1 。 当直线的斜率为90°时,直线的斜率不存在,它的方程不能用点斜式表示,但因l上每一点的横坐标都等于x 1 ,所以它的方程是x=x




直線方程式我想問第9題這題我看解答要計算斜率 Clear




直線方程式 斜率判斷例題 Youtube
一般式的斜率怎么算 k=A/B。 直线方程的一般式:AxByC=0(A≠0,B≠0)。 斜率是指一条直线与平面直角坐标系横轴正半轴方向的夹角的正切值,即该直线相对于该坐标系的斜率。一般式方程在计算机领域的重要性常用的直线方程有一般式 点斜式 截距式 斜截式 两点式等等。除了一般式方程,它们要么不能支持所有情况下的直线(比如跟坐标轴垂直或者平行),要么不能支持所有情况下的点(比如x坐标相等,或者y坐标相等)。所以一般式方程在用计算机处理二维图形数据方程式:y-y1=k(x-x1) 其中(x1,y1)为坐标系上过直线的一点的坐标,k为该直线的斜率。 推导:若直线L1经过点P1(x1,y1),且斜率为k,求L1方程。 设点P (x,y)是直线上不同于点P1的任意一点,直线PP1的斜率应等与直线L1的斜率,根据经过两点的直线的斜率



Page 13 Epd702 商職數學b影視版快易通 課本pdf




Shs 3 2斜率與一次函數的關係 Wmv Youtube
斜率截距式 任意直线方程的斜率截距式由下式给出: y = m x b 其中: m 是该线的斜率 b 是该线的y轴截距 通过任意两点(x 1 ,y 1 )和(x 2 ,y 2 )的直线的斜率 m 由下式给出: 线的y轴截距 b 是线与y轴交叉的点处的y值。 因为对于点(x 1 ,y 1 ),我们有y一般式的斜率怎么求 狮子TUOJIE 99人看过 今天让我们来了解一下,直线方程的一般式怎么求斜率吧~ 工具/原料 more 纸笔即可~ 了解一般式 首先我们要知道一般式的表达方式:AXBYC=0 求一般式斜率点斜式方程的方程公式 : 方程式yy1=k (xx1) 其中 (x1,y1)为坐标系上过直线的一点的坐标,k为该直线的斜率推导若直线L1经过点P1 (x1,y1),且斜率为k,求L1方程设点P (x,y)是直线上不同于点P1的任意一点,直线PP1的斜率应等与直线L1的斜率,根据经过两点的直线的斜率
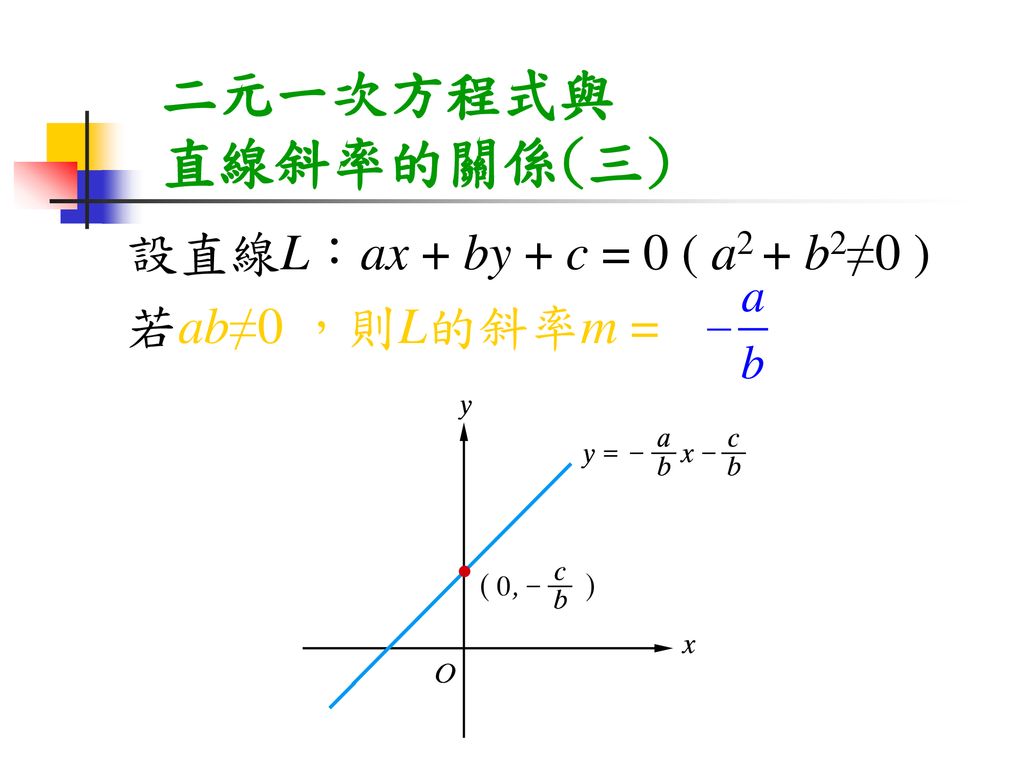



第一章直線 1 3 二元一次方程式的圖形 Ppt Download
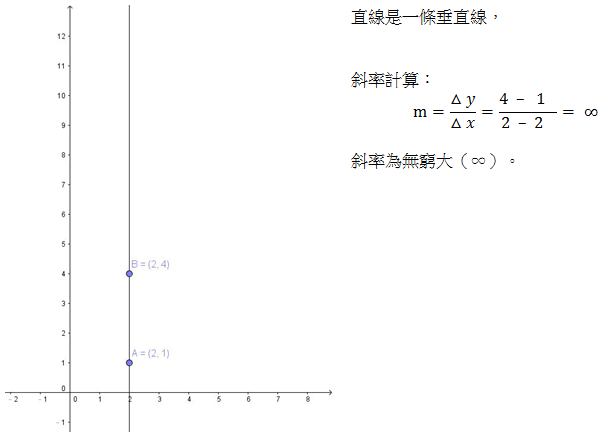



Scratch Math 直線裡的宇宙觀 二 在上一篇裡我們用蠻力搜尋法解決了水平直線的同一側兩點的最短路徑問題 蠻力搜尋法的 By Peter Wei Medium
摘要:在平面解析几何中,直线方程有多种形式,在解决不同的问题时,使用适当的方程形式可以使问题简化,本文将列举出这些方程即性质。 一般式: 一般式说明了平面直角坐标系上一个二元一次方程表示一条直线,这是一种一一对应的关系。 这里,a、b不同时为0,下面在表达斜率和截距时高二數學 圓的切線的方程 By 5sir on 16 年 11 月 15 日 圓和直線相切的充要條件 圓與直線相切 ⇔ d = r (心線距 = 半徑) ⇔ 公共點數目 = 1 求切線方程問題 (題型1) 已知切線經過 圓上 一點 >>所以: y = 2x 1 一些点的例子:
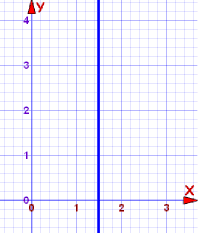



直线的方程




4种方法来求得一个方程的斜率
名称 方程 适用范围 点斜式 y-y1=k(x-x1) 不含垂直于x轴的直线 斜截式 y=kx+b 不含垂直于x轴的直线 两点式 = (x1≠x2,y1≠y2)不含垂直于坐标轴的直线 截距式 +=1 (ab≠0)不含垂直于坐标轴




直线方程 搜狗百科



已知斜率求方程已知斜率求方程



直线与方程 高中数学知识点 高考圈




4种方法来求直线方程



方程式斜率公式3 2 1 Deewi




4种方法来求得一个方程的斜率



方程y F X 表示的曲线曲线c的方程是f X Y 0 点p X0 Y0 不在曲线c上 则方程f X Y




2 3 平面上的直線與斜率 Ppt Download




4种方法来求直线方程



高中数学圆锥曲线 直线与抛物线 会用两种方法的都是高手 方程




數學的角落 直線方程式變化率 斜率 的解讀




數學公式 直線方程式的求法 已知線上兩點 博志bojhih 國中資優數學理化 痞客邦
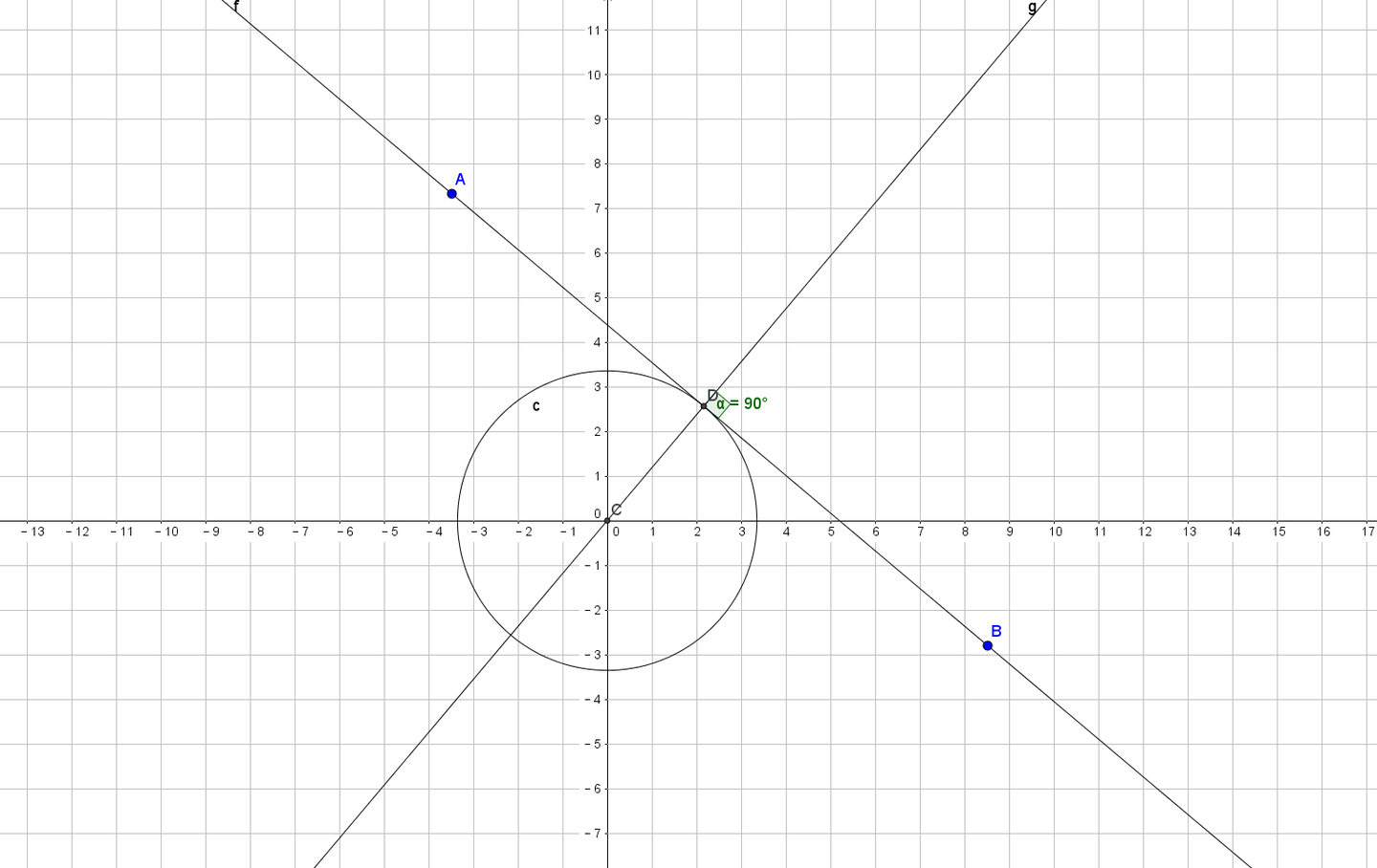



直线方程的各种形式 知乎




负数斜率怎么比较大小斜率为负值大小比较




2 1 直線方程式及其圖形直線的斜率1 直線的方程式2 兩直線關係直線方程式及其圖形page 1 Ppt Download
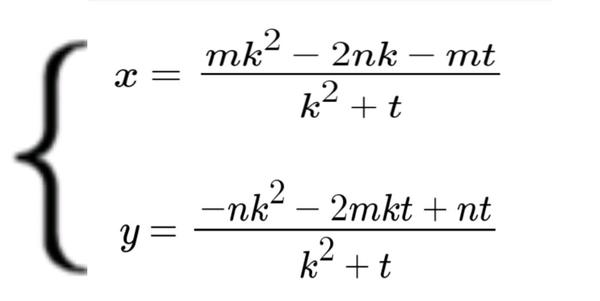



圆锥曲线关于斜率的参数方程 知乎



两点式公式斜截式 污表情 表情帝




數學方程式 Syj Math Works




标准方程的斜率




直線方程式 斜率的定義 斜角說明 Youtube




直线方程式找斜率 Youtube



直线方程斜率k的公式 扒拉扒拉




直线的方程



1



切线斜率公式 万图壁纸网




4种方法来求得一个方程的斜率



吳國平 高考數學直線方程問題不難 但很多人卻栽在這個小毛病上 雪花新闻



椭圆切线方程公式推导 初三网



直线的方程备考策略 斜率



切線方程式斜率transwiki 切線斜率 Rjrsw




2 1 直線方程式及其圖形直線的斜率1 直線的方程式2 兩直線關係直線方程式及其圖形page 1 Ppt Download



平面内的 直线方程 一览 知乎



如何用excel或wps计算直线的斜率和截距 Excel Exceloffice 微信公众号 水星excel




7 4 直線方程 從直線方程找出斜率 X截距及y截距 Youtube




2 1 2 直線的斜率舉例說明 Youtube



直线的方程




直线方程式 简书



直线与方程知识点总结 直线与方程知识点总结精选八篇 范文118
%20y=kx+b%E5%8F%AA%E9%97%9C%E4%BA%8E%E6%96%9C%E7%8E%87%E7%9A%84%E5%B0%B1%E9%80%99%E4%BA%9B%EF%BC%8C%E5%8F%AA%E9%9C%80%E6%8A%8A%E9%80%99%E5%85%A9%E5%80%8B%E4%BA%8C%E5%85%83%E4%B8%80%E6%AC%A1%E6%96%B9%E7%A8%8B%E8%81%AF%E7%AB%8B%E6%B1%82%E8%A7%A3%EF%BC%8C%E7%9B%B4%E7%B7%9A%E6%96%B9%E7%A8%8B%E6%98%AFx=x1%E3%80%82%20%E5%85%A9%E9%BB%9E%E5%BC%8F%E6%8E%A8%E5%B0%8E.%20%E6%88%91%E5%80%91%E7%9F%A5%E9%81%93%EF%BC%8Cw_794)



方程式斜率公式3 2 1 Deewi



函数点斜率的y截距斜线图png图片素材免费下载 图片编号 Png素材网



寻找斜率的方程是什么 教育小本子



腾讯视频



1




直線方程式 兩點式公式說明 Youtube




4种方法来求得一个方程的斜率



数学互动式教学讲义 教用 直线方程式及其图形 Doc 沃文网wodocx Com
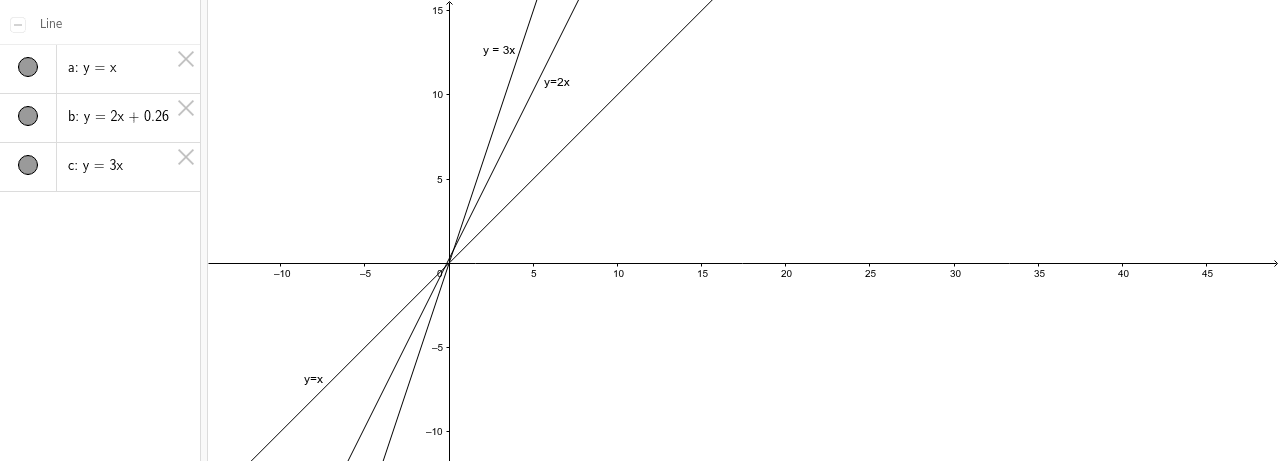



直線方程式 斜率比較 Geogebra




請問演練13的解答是什麼意思 看了好久還是不太懂 感謝 Clear




截距和 Ronia




4种方法来求得一个方程的斜率




直線方程式 斜率的定義說明 Youtube




怎么求切线方程切线方程例题 30高考网




高中數學 直線的方程 傾斜角以及斜率的取值範圍 每日頭條



农药名网 百科




标准方程的斜率




一元一次方程的斜率 一元一次方程的斜率代表什么 三人行教育网 Www 3rxing Org




线性方程斜率y截距公式 线png图片素材免费下载 图片编号 Png素材网




4种方法来求得一个方程的斜率




2 1 直線方程式及其圖形直線的斜率1 直線的方程式2 兩直線關係直線方程式及其圖形page 1 Ppt Download



Blog Archives 我的m讚




數學方程式 Syj Math Works



1



1



名師課輔網 平面上直線方程式的斜率




直線方程公式直綫方程 Qavhp




4种方法来求得一个方程的斜率




11 12 9 12 1 2 1 11 1 2 3 13 14 Chegg Com




4种方法来求得一个方程的斜率
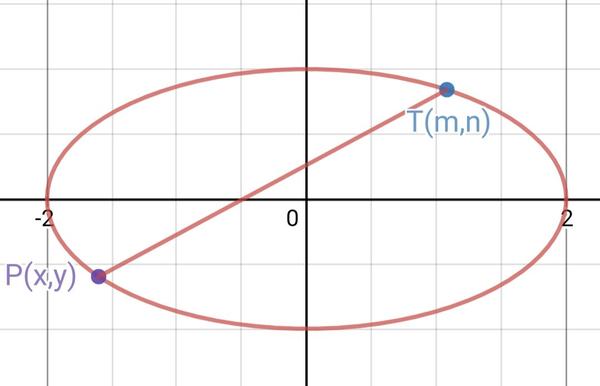



圆锥曲线关于斜率的参数方程 知乎




方程式斜率數學直線方程一般式中k 斜率 等于什么 作業幫 Mqttk



高考数学导数 求曲线在某点处的切线方程 通用解法一定要熟练 切点




曲線斜率公式直線方程式斜率公式 15點 急 Lvai




1 2 直线的方程 一 每日头条




标准方程的斜率



國中數學 斜率 直線 點斜式 兩點式 斜截式 截距式 平面性質 小葉白筆不是筆 痞客邦
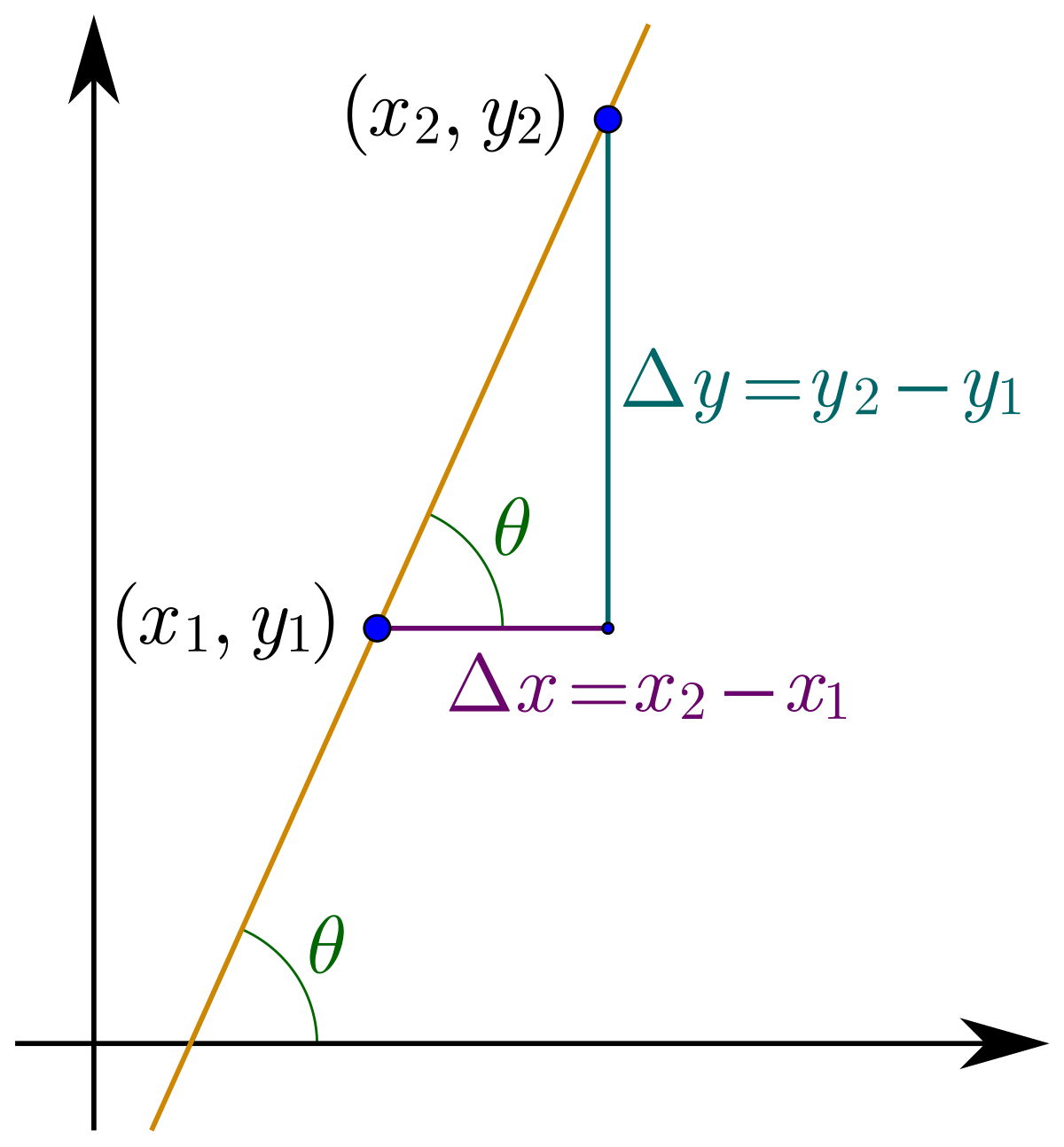



斜率 维基百科 自由的百科全书



直线配对 Activity Builder By Desmos



井民全觀點 Jing S Perspective 簡單的方法計算直線方程式using Python




學測 092 多選6 直線方程式的係數 評量專區 均一教育平台




4种方法来求得一个方程的斜率



0 件のコメント:
コメントを投稿