[コンプリート！] 面積の公式 sin 105231

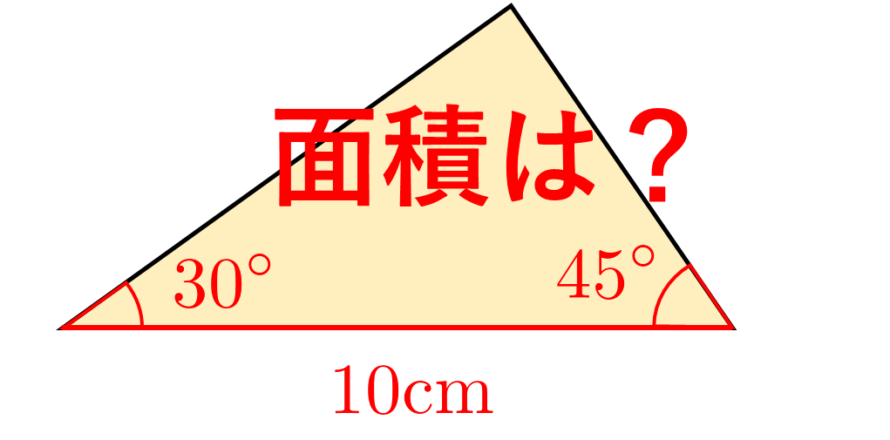
 ということで、面積公式を使うことができません こういう場合には、面積公式に必要な\(\sin\)の値を求めることからスタートします。 とは言っても、いきなり\(\sin\) の値を求めることは難しいので一旦、\(\cos\) の値を求める。三角関数を扱う場合には，積分に限らず次数に注目する必要があります。なぜなら，2倍角の公式や3倍角の公式 \\begin{array}t{l} \sin 2x = 2 \sin x \cos x \\ \cos 2x \begin{array}t{l} = \cos^2 x \sin^2 x \\ = 2\cos^2 x 1 \\ = 1 2\sin^2 x \end{array} \\ \displaystyle \tan 2x = \frac{2 \tan x}{1 \tan^2 x} \\8px \cos 3x = 4 \cos^3 x 3 \cos底辺×高さ÷2＝面積 a×h 2 1 a h 台形の面積 （上底下底）×高さ÷2＝面積 （ab ）×h 2 1 h（ab ） 平行四辺形の面積 底辺×高さ＝面積 a×h=a h ひし形の面積 対角線×対角線÷2＝面積 a×b 2 1 a b 円の面積

正三角形の面積の求め方 小学生用 高校生用 具体例で学ぶ数学

面積の公式 sin

面積の公式 sin-三角形面積公式 三角形面積的求解有數種不同的方法，但這些方法分散在不同章節裡。 我們應將這些公式彙整在一起，方便自己比較、使用與記憶。 以下羅列三角形面積（ ）重要的求解公式： 基本公式 ＝1/2底×高 海龍公式 ＝√s（sa）（sb）（sc） s＝a sin・cos・tanの重要公式3つ sin・cos・tanの間には重要な公式があります。 三角関数の分野ではこれから頻繁に使うことになるので、 必ずこれから紹介する公式は暗記しておきましょう！ 三角関数の公式その1 公式の1つ目は、 sin 2 θ cos 2 θ = 1 です。

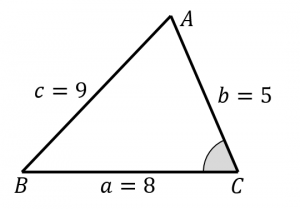
三角形の面積を３辺の長さから求める２つの方法 具体例で学ぶ数学

 こんにちは、ウチダです。 今日は、小学生から高校生まで通して学ぶ 「三角形の面積の求め方」 について、まずは基本から入り、徐々に高校数学の内容に進化させていきます。 具体的には、数学Ⅰで習う "sin" を用いる公式や、数学Bで習う "ベクトル" を用いる公式について、詳しく解説し正弦定理を三角形の面積と関連付けます。 ※ 図は Markdown に SVG を直接記述しています。詳細はこちらをご参照ください。 正弦定理 図 1 A B C 2R a b c 教科書でよく見る形の正弦定理は、円の直径との関係を含んだ形で記述されます。そうであれば、ラジアンに直して、公式に代入ください。参考）角度の換算 度≒ ラジアンなので、 例えば面積 S=1/2*()^2*(sin())= と求められます。

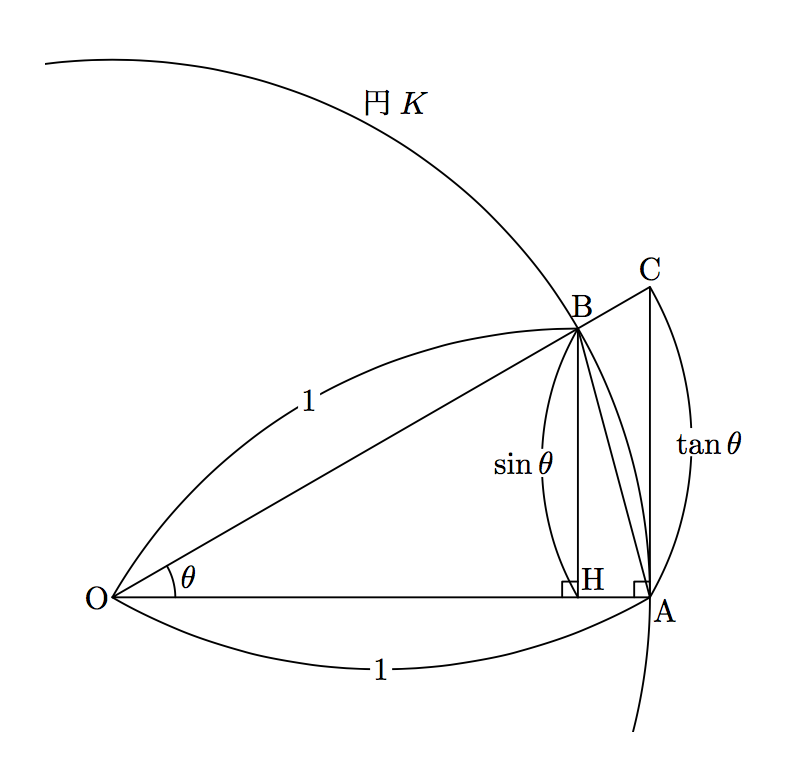
Sinθ = 1 となり、lim θ!0 sinθ θ = 1 が得られる。sin(¡θ) ¡θ = sinθ θ なので、θ < 0 での極限も同じ値となる。 ⁄ この証明における不備は、扇形OAP の面積がθ 2 となるところにある。 もう少し詳しく説明すると、扇形の面積の公式 扇形の面積= (弧長£ 半径)¥2Sin q ， cos q の 0 から p / 2 までの定積分すなわち面積は である．そして， cos q は sin q を p / 2 平行移動したものでありかつ周期関数である．この性質を理解すれば角度 0 から， n p /2 ： n は整数，の定積分値が簡単にわかる．面積（英語： Area ）是用作表示一個曲面或平面 圖形所佔範圍的量，可看成是長度（一維度量）及體積（三維度量）的二維類比。 對三維立體圖形而言，圖形的邊界的面積稱為表面積。 計算各基本平面圖形面積及基本立體圖形的表面積公式早已為古希臘及古中國 人所熟知。

，則三角形面積公式為 8， 1/2*a*h(a邊上的高)1/2*a*b* sin角ACB 三角形面積的公式(關于三角函數的)高一必修4作業幫 ，三角形，此 三角形面積公式余弦定理 三角形面積公式(正余弦) ，三角形面積公式即兩夾邊之積乘夾角的正弦值再除以2。この公式にx(t), y(t) を適当な関数を設定し、展開すると面積Sが得られます。 x(t) = A sin (ωt)、y(t) = B sin(ωt φ)とおいて計算してみると・・・ s= π*AB * sinφとなるはずです。 では面積Sが別の方法で判明すれば、上の式からsinφをもとめるヒントとなるでしょう。 楕円の面積の公式は、主に \(2\) 通りの方法で導くことができます。 証明①図形の拡大・縮小 \(1\) つ目は、図形の拡大・縮小の考え方を利用します。 ただし、この証明では円の面積の公式が成り立つことが前提です。

ブレートシュナイダーの公式 四角形の面積 大学入試数学の考え方と解法

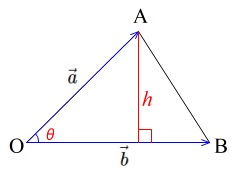
ベクトルの大きさと内積だけで表す面積の公式

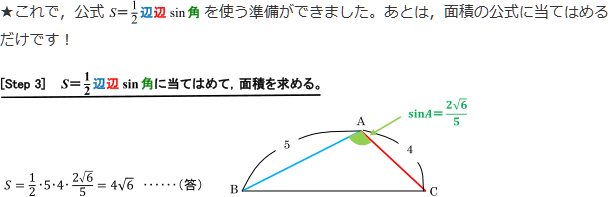
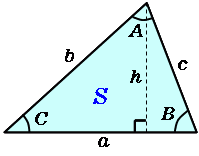
回転体の表面積の公式 (Ⅰ) 区間a，b で連続，区間(a，b) で微分可能な曲線 y ＝f (x) とx 軸 とで挟まれる図形を x 軸のまわり に回転してできる回転体の曲面の 表面積S は，次式で計算できる。 S ＝2π∫ a b y √ 1＋(dy dx) 2 dx (Ⅱ) 区間c，d で連続，区間(c，d)例子：这个三角形的面积是多少？ （注意：12 是 高，不是左边的长度） 高 = h = 12 底 = b = 面积 = ½ bh = ½ × × 12 = 1面積を求めるときは，公式　S＝1/2 bc sin A に当てはめればいいことは知っています。

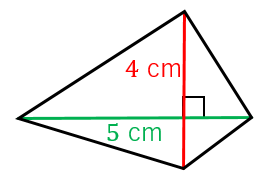
四角形の対角線の長さから面積を求める公式 具体例で学ぶ数学

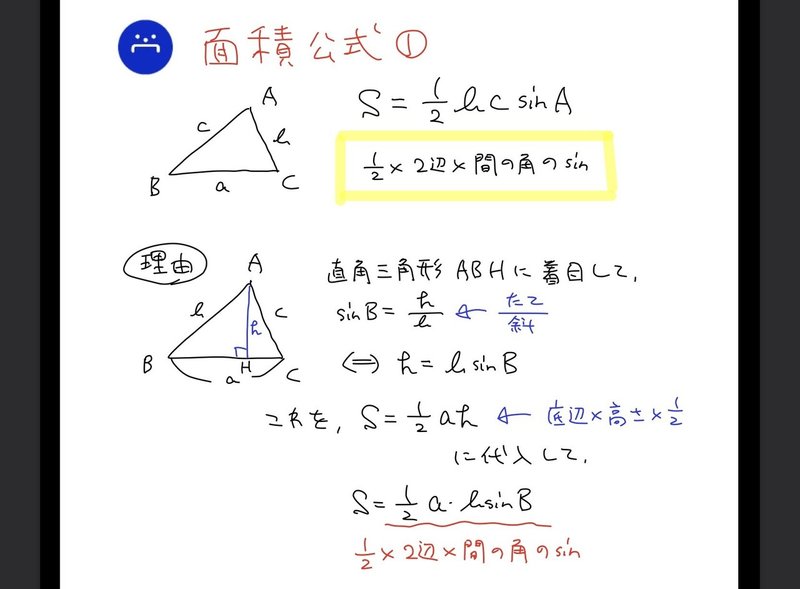
高校数学無料問題集 数 第３章 図形と計量 面積 桝 ます Note

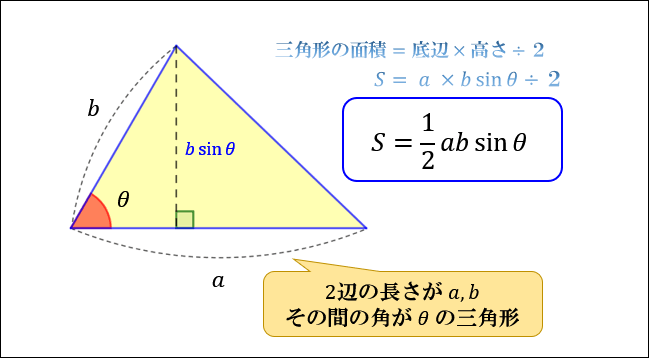
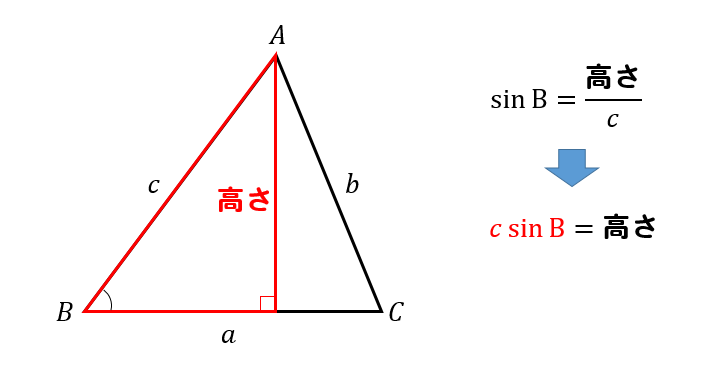
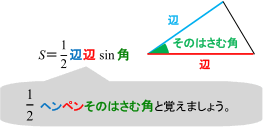
 三角関数の2倍角の公式・半角の公式の証明と応用 スポンサーリンク 高校数学Ⅱ 三角関数 検索用コード 証明は容易で,\ \bm {加法定理において\ \beta\ →\ \alpha\ }とするだけである \bm {利用機会が極めて多い}ので,\ 毎回加法定理から導くというのは當我們有一個三角形，邊長與角度如上圖所示時，則面積會等於一半的兩邊乘上夾角的 $ sin $ 值：$$ 面積 =\frac{1}{2}\cdot a\cdot b\cdot sin(\angle C) $$三邊長與對角的關係呈：$$ \frac{a}{sin\angle A} = \frac{b}{sin\angle B} = \frac{c}{sin\angle C} $$任意一邊長與另外兩邊的關係為：$$ c^2 = a^2 b^2 2\cdot a\cdot b\cdot cos\angle Cポイントに従って、平行四辺形の面積公式を使ってみよう。 中学校までは、（底辺）×（高さ）で求めたね。 数学Ⅰでは、（高さ）を 「（斜めの辺）×sin」 で表すよ。

高校数学 正多角形の面積の求め方 例題編 映像授業のtry It トライイット

高校数学 三角形の外接円の半径 内接円の半径と面積の関係 S 1 2r A B C 受験の月

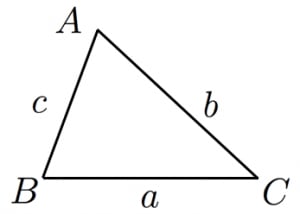
 三角形の面積にまつわる公式 ヘロンの公式 まずはおなじみ，三角形の三辺の長さから面積を求めるヘロンの公式。 外接円の半径と三角形の面積の関係 S = a b c 4 R S=\dfrac{abc}{4R} S = 4 R ab c 公式。これもなかなか使い勝手が良い公式。この公式自体に三角関数は現れませんが、上の sin を用いた面積公式と、余弦定理から導かれています。 2直線のなす角と傾きの関係 2直線の傾きとその間の角 θ に関して、次の式が成り立ちます。公式集（数学Ⅱ・B） 頭に入っていますか？ ⑧ 和積の公式 2 cos 2 sin sin 2sin A B A B A B = 2 sin 2 sin sin 2cos A B A B A B = 2 cos 2 cos cos 2cos A B A B A B = 2 sin 2 cos cos 2sin A B A B A B =⑨ 三角関数の合成 q q=a b r qasin cos sin( ) ただし、 = r a b 2 2 2 2 sin

高校数学 平行四辺形の面積の求め方 例題編 映像授業のtry It トライイット

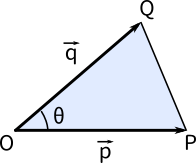
数bベクトル ベクトルで作る三角形の面積を導出する Mm参考書

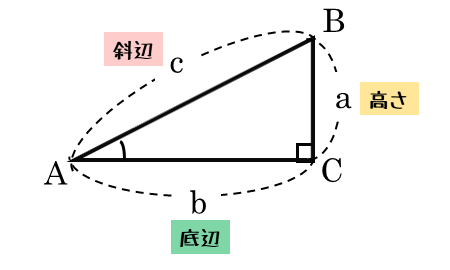
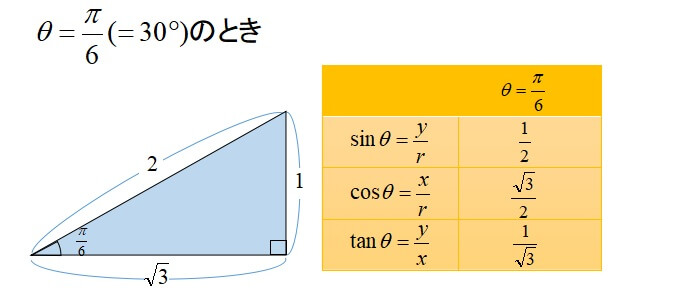
 二等辺三角形の一辺から 直角に線 を引き、 高さ を作ります。 高さの長さを求める 補助線により出来た三角形は、 30°, 60°, 90°の直角三角形 です。 この 三角形は 一番長い辺と一番短い辺の 長さの比が 2 1 になっています。 ※ 30°, 60°, 90°の三角形(三角定規)の長さの比 は 覚えておいSinを使った面積公式 三角関数を使って 三角形の面積を求めることもできるんです。 sin（サイン）を用いた面積公式は三角形の2辺とその間の角が分かってるときに使うことができます。積分 sinθ の図形による理解 ∫ sinθdθ ∫ sin ⁡ θ d θ の積分を図形を用いて直感的に理解する． 左側の図は 単位円 ，右側の図は y =sinθ y = sin ⁡ θ のグラフである． 図において赤色の面積と青色の面積は等しい． ∫ π 2 0 sinθdθ =−cosθπ 2 0 = −cos π 2

三角形の面積を求める公式７選 高校数学のまとめにどうぞ

ベクトルによる三角形の面積の求め方 公式や証明 計算問題 受験辞典

三角関数は周期関数なので、逆関数は多価関数である。 逆関数の性質から以下が成り立つ： =,() = / /ピタゴラスの定理 ピタゴラスの定理やオイラーの公式などから以下の基本的な関係が導ける 。 = ここで sin 2 θ は (sin(θ)) 2 を意味する。 この式を変形して、以下の式が導かれる：公式(4)の中に出てくるーcotとは－cosのことでしょうか？ ＝＞作者：連絡ありがとう．今の高校の教科書では sinθ,cosθ,tanθまでは書かれていますが，それらの逆数 cosecθ,secθ,cotθは書かれていないのが普通です．（学習指導要領からの逸脱と言われないように，言ってはならないと自己検閲して 他の面積公式との関係 この面積公式をもとに他の面積公式を導出することができます。 例えば，この公式と正弦定理を用いることで対称な式： S = a b c 4 R S=\dfrac{abc}{4R} S = 4 R ab c を得ることができます（ R R R は三角形 A B C ABC A BC の外接円の半径）。

三角形の面積 三角比 Geogebra

Sinを用いた三角形の面積公式 高校数学の美しい物語

この を計算すると，負になってしまったのですね。 面積ですから負になるのはおかしいです。 計算間違いをしていることも考えられますが，公式を利用するときに間違えている可能性が高いです。 具体例を参考にしてみてください。 放物線 y = x2 3 x と面積公式 sin ookkk3 ookkk3 10 主題一，三角形面積公式 Show 8 PDF 檔案主題一，三角形面積公式 若 a﹐b 和 c 分別表 ABC 三內角 A﹐ B 和 C 的對邊長﹐ 表示 ABC 的面積﹐則 1 1 1 sin sin sin 2 2 2 bc A ca B ab C ﹒ 例題1 在 ABC 中﹐已知 AB 10﹐AC 8﹐ A 1﹐ 求 ABC的

数学ia 三角形の面積を理解しましょう Himokuri

ベクトルの三角形の面積公式を超わかりやすく説明した 理系ラボ

なぜsinなのですか Clear

高校数 三角比 三角形の面積の公式 オンライン無料塾 ターンナップ Youtube

三角形の面積の三角比を用いた公式 数学の偏差値を上げて合格を目指す

3

簡単 三角錐の体積 表面積の求め方と展開図が誰でもすぐわかる記事 高校生向け受験応援メディア 受験のミカタ

正三角形の面積の求め方 小学生用 高校生用 具体例で学ぶ数学

三角形の面積の求め方とは Sinやベクトルを用いる公式も解説 小学生から高校生まで 遊ぶ数学

数学 三角比 Sin Cos Tanの面積公式と覚え方 理系ラボ

平行四辺形の面積 ベクトルでの公式 理数系無料オンライン学習 Kori

高校数学 三角比 三角比を使った三角形の面積の求め方 Sin Cos ヘロンの公式を使った方法 数学の面白いこと 役に立つことをまとめたサイト

四角形の面積の公式ですか これは数学のどこの範囲ですか Clear

数学 三角比 Sin Cos Tanの公式まとめ 表 変換 相互関係 面積 正弦定理 余弦定理 理系ラボ

48s96ub7b0z5f Net Kuukan Bekutoru Menseki

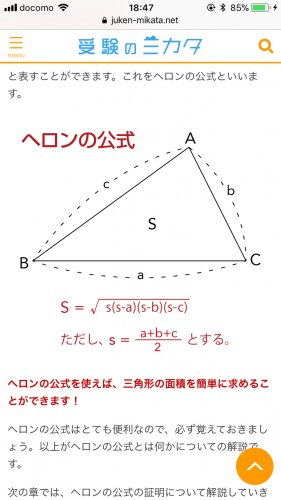
ヘロンの公式なんですが Sって面積のことですよね なのにs 2分のa B 高校受験 教えて Goo

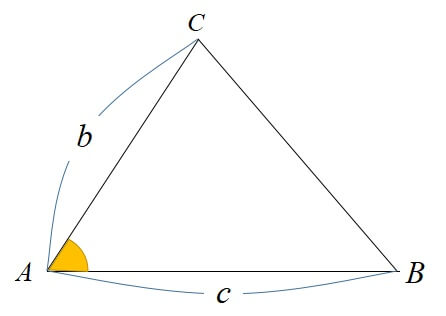
Sin サイン を用いる三角形の面積公式を解説

高校数学 円に内接する四角形の対角線の長さと面積 受験の月

極方程式の面積 扇形積分 おいしい数学

高校数学 平行四辺形の面積の求め方 例題編 映像授業のtry It トライイット

図形と計量 三角形の3辺が与えられたときの面積の求め方 数学 定期テスト対策サイト

三角形とは 面積公式 角度 辺の長さ 重心 比の計算 受験辞典

三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ

高校数 三角比 三角形の面積 ３辺の長さから オンライン無料塾 ターンナップ Youtube

三角形の面積を三辺から求める公式 Schoolmath S Diary

三角形の3辺が与えられたときの面積の求め方 数学 苦手解決q A 進研ゼミ高校講座

Sinを用いた三角形の面積公式 高校数学の美しい物語

ヘロンの公式とは 図解でわかるその仕組みと証明方法 アタリマエ

ヘロンの公式とは 証明や 四角形版 ブラーマグプタの公式 も 受験辞典

三角比を用いた面積計算をマスターしよう スタディクラブ情報局

台形の面積の求め方 公式が誰でも一目でわかる 練習問題付き 高校生向け受験応援メディア 受験のミカタ

外接円とは 半径の公式や求め方 性質 書き方 受験辞典

余弦定理まとめ 公式 面積 問題と解き方 理系ラボ

ヘロンの公式で三角形の面積を求める 三辺の長さがわかっているときはコレ 数学の面白いこと 役に立つことをまとめたサイト

三角関数の極限公式とその証明 おいしい数学

計算

高校数学 正多角形の面積の求め方 練習編 映像授業のtry It トライイット

この解き方で求める手順はあっていますか またコサインしか分かっていないのに Sinが Clear

面積の求め方 計算公式一覧

Sinを用いた三角形の面積公式 高校数学の美しい物語

3

ヘロンの公式 三辺から面積を求める をシミュレーターを使って理解しよう 数学入門

高校数学 座標平面上の三角形の面積の公式 受験の月

三角形の辺や角が与えられたとき残りの辺や角を求める方法 数学の偏差値を上げて合格を目指す

三角形の面積を３辺の長さから求める２つの方法 具体例で学ぶ数学

数学 三角比 Sin Cos Tanの面積公式と覚え方 理系ラボ

Sin8 8 1 の高校での証明は循環論法ではない Saitei Net

扇形の面積公式が一目でわかる 丁寧な証明付き 高校生向け受験応援メディア 受験のミカタ

三角形の面積

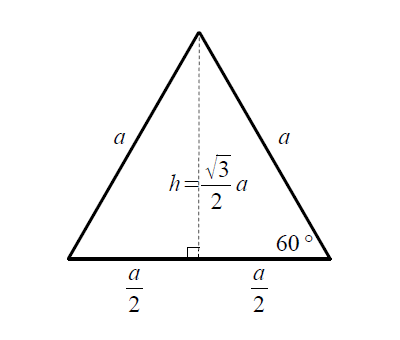
正三角形の面積計算 ゆるゆるプログラミング

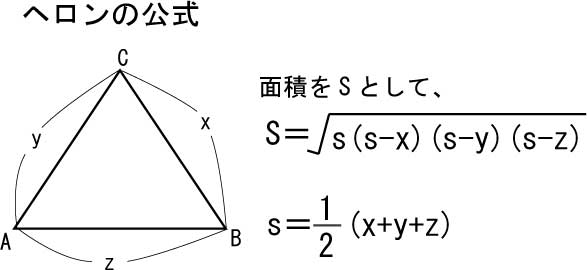
正弦定理 余弦定理の求め方 三角形いろいろ 三角比の応用 エミュー

1

高校数学でよく使う三角形の面積公式まとめ おいしい数学

三角比の公式まとめ サイン コサイン タンジェント 正弦定理 余弦定理など Irohabook

四角形の面積の公式ですか これは数学のどこの範囲ですか Clear

高校数学 ３辺 三角形の面積 を求める方法 例題編 映像授業のtry It トライイット

簡単 正三角形の面積公式が一瞬で分かる 見やすい図で徹底解説 高校生向け受験応援メディア 受験のミカタ

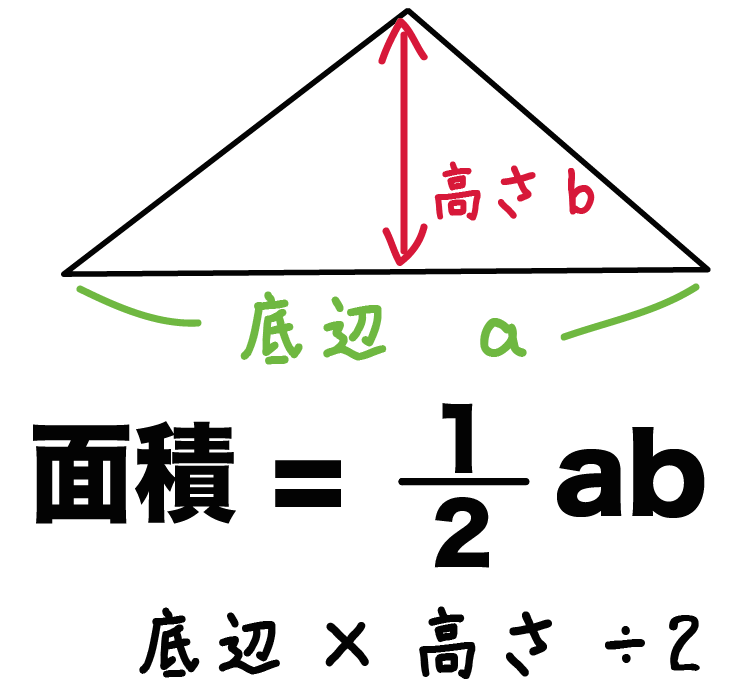
簡単公式 三角形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ

サイン Sin を使って三角形の面積を求める練習問題一覧 数学i By ふぇるまー マナペディア

四角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ

三角比を使って三角形の面積を求める方法 数学i By Okボーイ マナペディア

円弧面積の計算式

三角形の面積の求め方まとめ 数学の偏差値を上げて合格を目指す

三角形面積公式 正弦 引入 Youtube

なぜ円の面積 P 半径 半径 なのでしょうか 簡単に証明方法はあるのでしょうか Quora

高校数学 直角三角形を用いた三角比 Sin8 Cos8 Tan8 の定義とその理由 30 45 60 の三角比 受験の月

三角法とは コトバンク

わかりやすい三角比と基本公式 Irohabook

三角形の面積を外接円の半径を使って求める Schoolmath S Diary

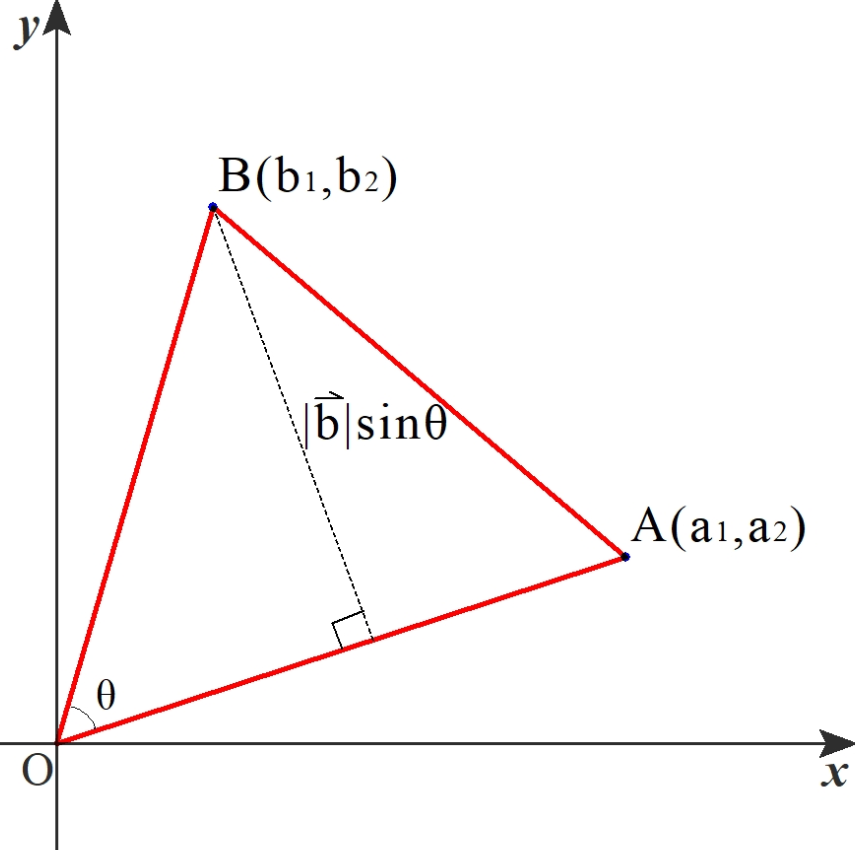
ベクトルを用いた三角形の面積公式3種類 数学の庭

弓形の面積 香料ゐっすゐの夢

48s96ub7b0z5f Net Bekutoru Menseki

高校 数学i 図形と計量 三角形の面積sinの利用 Youtube

三角形の合同条件と面積 数学 統計教室の和から株式会社

三角関数の公式一覧

三角比の面積 公式と計算方法は いろんな場面での使い方を解説 数スタ

面積の求め方 計算公式一覧

数学 三角比 Sin Cos Tanの面積公式と覚え方 理系ラボ

正弦定理と余弦定理の使い方と面積の公式

図形と計量 三角形の面積について 日々是鍛錬 ひびこれたんれん

中学 高校で習う三角形の面積公式 Memory Map 数学 化学講師 佐藤学による受験生に役立つ濃縮ポイントと Etc

三角形の3辺が与えられたときの面積の求め方 数学 苦手解決q A 進研ゼミ高校講座

三角比まとめ 完全攻略

Q Tbn And9gcq7h6dlzvq5e0plulfvxu64dpvadasyky0sizoi2drjv Uyz1m5 Usqp Cau

高校数学 ３辺 三角形の面積 を求める方法 例題編 映像授業のtry It トライイット

とどろき英数塾 高校生のページ 公式集 三角比と三角関数

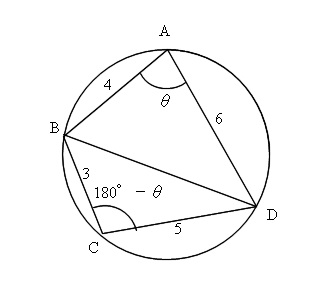
円に内接する四角形の面積の求め方と定理の使い方

3 10 三角形面積公式的推導 Youtube

空間図形に含まれる三角形の面積を求める問題 直方体 数学i By ふぇるまー マナペディア

高校数学 三角形の面積の公式 映像授業のtry It トライイット

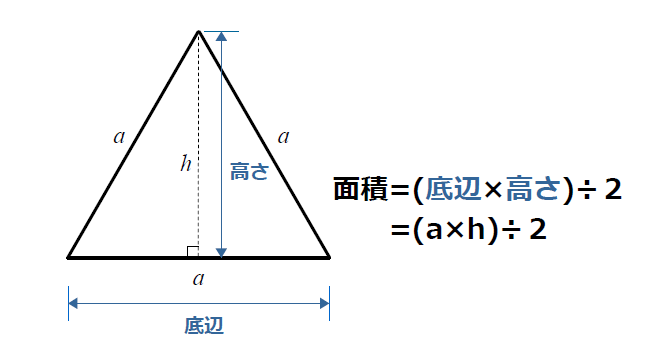
正三角形の面積計算 ゆるゆるプログラミング